题目内容
16.集合{y|y=$\frac{6}{x+3}$,x∈Z,y∈Z}的元素的个数为8.分析 依据题意知,$\frac{6}{x+3}$只能为±1、±2、±3、±6,分别求出x即可.
解答 解:由于y=$\frac{6}{x+3}$∈Z,x∈Z,则$\frac{6}{x+3}$只能为±1、±2、±3、±6,
当$\frac{6}{x+3}$=1时,x=3;
当$\frac{6}{x+3}$=-1时,x=-9;
当$\frac{6}{x+3}$=2时,x=0;
当$\frac{6}{x+3}$=-2时,x=-6;
当$\frac{6}{x+3}$=3时,x=-1;
当$\frac{6}{x+3}$=-3时,x=-5;
当$\frac{6}{x+3}$=6时,x=-2;
当$\frac{6}{x+3}$=-6时,x=-4;均满足题意.
故集合{y|y=$\frac{6}{x+3}$,x∈Z,y∈Z}的元素的个数为8个,
故答案为:8
点评 本题考查元素与集合关系的判断等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
6.圆锥的母线长为l,高为$\frac{1}{2}$l,则过圆锥顶点的最大截面的面积为( )
| A. | $\frac{\sqrt{3}}{4}$l2 | B. | $\frac{1}{2}$l2 | C. | $\frac{\sqrt{3}}{2}$l2 | D. | $\frac{1}{4}$l2 |
14.“a=-1”是“过点P(2,1)有且只有一条直线与圆R:x2+y2+2ax+ay+2a2+a-1=0相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
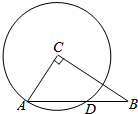 如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.
如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.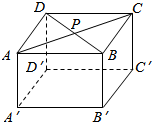 如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )
如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )