题目内容
如图,在 中,
中, ,
, ,
, ,点
,点 是
是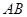 的中点.
的中点.
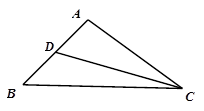
(1)求边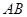 的长;
的长;
(2)求 的值和中线
的值和中线 的长
的长
 中,
中, ,
, ,
, ,点
,点 是
是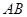 的中点.
的中点.
(1)求边
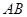 的长;
的长;(2)求
 的值和中线
的值和中线 的长
的长(1) (2)
(2)
 (2)
(2)
试题分析:(1)由题意,
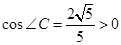 ,可知
,可知 是锐角,由平方关系求出
是锐角,由平方关系求出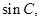 ,由正弦定理即可求出
,由正弦定理即可求出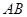 的长;
的长;(2)因为
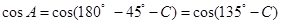 ,由(1)可知
,由(1)可知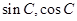 ,展开即可求出
,展开即可求出 的值,而中线
的值,而中线 直接代入余弦定理即可.
直接代入余弦定理即可.(1)在
 中,由
中,由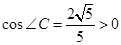 可知,
可知, 是锐角,
是锐角,所以,
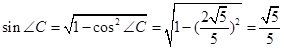
由正弦定理
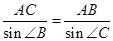

(2)
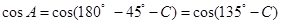
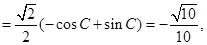
由余弦定理:
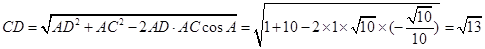

练习册系列答案
相关题目
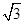 sinA)cosB=0.
sinA)cosB=0. ,BD=
,BD= ,周长为18,则这个平行四边形的面积为( )
,周长为18,则这个平行四边形的面积为( )
 ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
. 斜边AB上的三等分点,则tan
斜边AB上的三等分点,则tan ECF=( )
ECF=( )

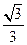

 ,
, ,
, ,则
,则 等于( )
等于( )

