题目内容
【题目】已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=（ 
）x ．
（1）求当x＞0时f（x）的解析式；
（2）画出函数f（x）在R上的图象； 
（3）写出它的单调区间．
【答案】
（1）解：若 x＞0，则﹣x＜0…
∵当x＜0时，f（x）=（ 
）x．
∴f（﹣x）=（ ）﹣x．
∵f（x）是定义在R上的奇函数，
f（﹣x）=﹣f（x），
∴f（x）=﹣（ ）﹣x=﹣2x
（2）解：∵（x）是定义在R上的奇函数，
∴当x=0时，f（x）=0，
∴f（x）=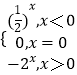 
．
函数图象如下图所示：
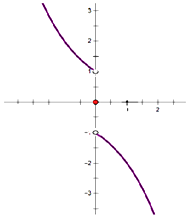
（3）解：由（2）中图象可得：f（x）的减区间为（﹣∞，+∞）；
无增区间
【解析】（1）若 x＞0，则﹣x＜0，根据x＜0时，f（x）=（ ）x ． 奇函数满足：f（﹣x）=﹣f（x），可得当x＞0时f（x）的解析式；（2）由（1）可得函数的解析式，结合指数函数的图象和性质，可画出函数f（x）在R上的图象；（3）由（2）中图象，可得函数的单调区间．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
