题目内容
【题目】函数f(x)=Asin(ωx+φ) ![]() 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)﹣cos2x,求函数g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.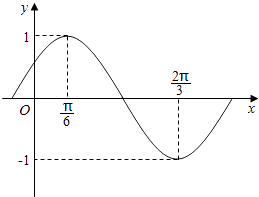
【答案】解:(Ⅰ)由图可得A=1, ![]() ,所以T=π.
,所以T=π.
所以ω=2.
当 ![]() 时,f(x)=1,可得
时,f(x)=1,可得 ![]() ,
,
因为 ![]() ,所以
,所以 ![]()
所以f(x)的解析式为 ![]() .
.
(Ⅱ) ![]()
= ![]()
= ![]() =
= ![]() .
.
因为 ![]() ,所以
,所以 ![]() .
.
当 ![]() ,即
,即 ![]() 时,g(x)有最大值,最大值为1;
时,g(x)有最大值,最大值为1;
当 ![]() ,即x=0时,g(x)有最小值,最小值为
,即x=0时,g(x)有最小值,最小值为 ![]()
【解析】(Ⅰ)由图可得A=1,一个周期内最高点与最低点的横坐标之差的绝对值为半个周期,得最小正周期T,进而得ω,代入最高点坐标求φ,得f(x)的解析式;(Ⅱ)由(Ⅰ)知f(x)的解析式,代入求出g(x)的解析式,用两角和的正弦公式把式中的第一项展开,合并,再逆用两角差的正弦公式把式子变形为一个角的一个三角函数值,由x的范围,得到2x﹣ ![]() 的范围,由正弦函数的图象得到sin(2x﹣
的范围,由正弦函数的图象得到sin(2x﹣ ![]() )的最大值和最小值.
)的最大值和最小值.
【考点精析】利用三角函数的最值对题目进行判断即可得到答案,需要熟知函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目