题目内容
【题目】已知椭圆
，离心率为
，两焦点分别为
，过
的直线交椭圆
于
两点，且
的周长为8.
（1）求椭圆
的方程；
（2）过点
作圆
的切线
交椭圆
于
两点，求弦长
的最大值．
【答案】（1）
（2）
【解析】试题分析：（1）求椭圆标准方程，一般利用待定系数法，即根据条件列两个独立方程：一是离心率
，二是椭圆定义： 
的周长为
，解方程组得
， 
（2）涉及弦长问题，一般利用直线方程与椭圆方程联立方程组，结合韦达定理和弦长公式求弦长：设切线
的方程为
，则
，再根据直线与圆相切得
，即
，代入化简得
，最后利用基本不等式求最值
试题解析：（1）由题得： 
，．．．．．．．．．．．．．．．．．．．．．．．．1分
，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
所以
．．．．．．．．．．．．．．．．．．．．．．．．．4分
又
，所以
，．．．．．．．．．．．．．．．．．．．．．．．．5分
即椭圆
的方程为
．．．．．．．．．．．．．．．．．．．．6分
（2）由题意知， 
，设切线
的方程为
，
由
，得
．．．．．．．．．．．．．．．7分
设
，
则
．．．．．．．．．．．．．．．．．．．．．8分
，
由过点
的直线
与圆
相切得
，即
，
所以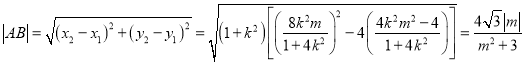
．．．．11分
，
当且仅当
时， 
，所以
的最大值为2．．．．．．．．．．．．．．．．．．．12分
练习册系列答案
相关题目
