题目内容
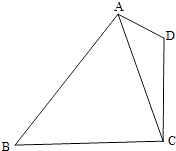
【题目】如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C． 
（1）证明：AC=AB1；
（2）若AC⊥AB1 ， ∠CBB1=60°，AB=BC，求二面角A﹣A1B1﹣C1的余弦值．
【答案】
（1）证明：连结BC1，交B1C于点O，连结AO，
∵侧面BB1C1C为菱形，
∴BC1⊥B1C，且O为BC1和B1C的中点，
又∵AB⊥B1C，∴B1C⊥平面ABO，
∵AO平面ABO，∴B1C⊥AO，
又B10=CO，∴AC=AB1，
（2）解：∵AC⊥AB1，且O为B1C的中点，∴AO=CO，
又∵AB=BC，∴△BOA≌△BOC，∴OA⊥OB，
∴OA，OB，OB1两两垂直，
以O为坐标原点， 
的方向为x轴的正方向，| |为单位长度，
的方向为y轴的正方向， 
的方向为z轴的正方向建立空间直角坐标系，
∵∠CBB1=60°，∴△CBB1为正三角形，又AB=BC，
∴A（0，0， 
），B（1，0，0，），B1（0， ，0），C（0， 
，0）
∴ 
=（0， ， ）， 
= 
=（1，0， ）， 
= 
=（﹣1， ，0），
设向量 
=（x，y，z）是平面AA1B1的法向量，
则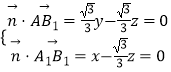 
，可取 =（1， 
， ），
同理可得平面A1B1C1的一个法向量 
=（1，﹣ ， ），
∴cos＜ ， ＞= 
= 
，
∴二面角A﹣A1B1﹣C1的余弦值为
【解析】（1）连结BC1 ， 交B1C于点O，连结AO，可证B1C⊥平面ABO，可得B1C⊥AO，B10=CO，进而可得AC=AB1；（2）以O为坐标原点， 的方向为x轴的正方向，| |为单位长度， 的方向为y轴的正方向， 的方向为z轴的正方向建立空间直角坐标系，分别可得两平面的法向量，可得所求余弦值．
