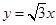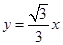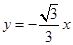题目内容
[2012·湖北高考]过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分成两部分,使得这两部分的面积之差最大,则该直线的方程为( )
| A.x+y-2=0 | B.y-1=0 |
| C.x-y=0 | D.x+3y-4=0 |
A
解析

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
直线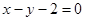 被圆
被圆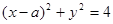 截得的弦长为
截得的弦长为 ,则实数
,则实数 的值为 ( )
的值为 ( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或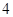 |
过点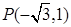 的直线
的直线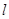 与圆
与圆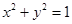 有公共点,则直线
有公共点,则直线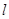 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A.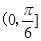 | B.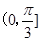 | C.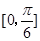 | D.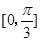 |
已知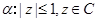 ,
,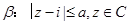 .若
.若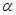 是
是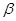 的充分非必要条件,则实数
的充分非必要条件,则实数 的取值范围是( )
的取值范围是( )
A.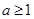 | B.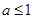 | C.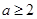 | D.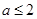 |
若直线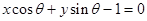 与圆
与圆 相切,且
相切,且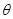 为锐角,则这条直线的斜率是( )
为锐角,则这条直线的斜率是( )
A.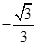 | B.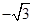 | C. | D.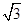 |
若点P(3,-1)为圆(x-2)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A.x+y-2=0 | B.2x-y-7=0 |
| C.2x+y-5=0 | D.x-y-4=0 |
若圆O的半径为3,直径AB上一点D使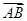 =3
=3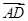 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则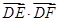 =( )
=( )
| A.-3 | B.-4 | C.-6 | D.-8 |
已知圆 与圆
与圆 相外切,则
相外切,则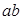 的最大值为( )
的最大值为( )
A.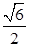 | B.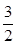 | C.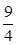 | D.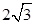 |
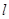 经过坐标原点,且与圆
经过坐标原点,且与圆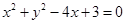 相切,切点在第四象限,则直线
相切,切点在第四象限,则直线