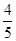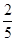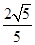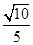题目内容
若直线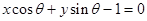
与圆
相切，且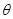
为锐角，则这条直线的斜率是( )
A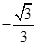． | B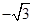． | C． | D． |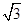
A
解析试题分析：解:由题意：
，
所以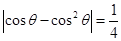
，
因为且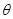为锐角，所以
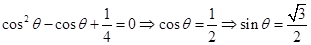
所以直线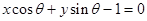的斜率是
故选A．
考点：1、直线与圆的位置关系；2、同角三角函数基本关系．
练习册系列答案
高中必刷题系列答案
相关题目
直线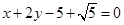
被圆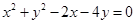
截得的弦长为 （ ）
| A．1 | B．2 | C．3 | D．4 |
设A为圆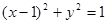
上的动点，PA是圆的切线且|PA|=1，则P点的轨迹方程是 （ ）
A． | B． |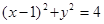
C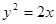． | D． |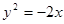
若直线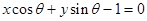
与圆
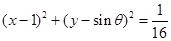相切，且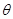
为锐角，则这条直线的斜率是( )
A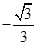． | B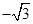． | C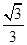． | D． |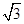
已知M(－2,0)，N(2,0)，则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A．x2＋y2＝2 | B．x2＋y2＝4 |
| C．x2＋y2＝2(x≠±2) | D．x2＋y2＝4(x≠±2) |
[2012·湖北高考]过点P(1,1)的直线，将圆形区域{(x，y)|x2＋y2≤4}分成两部分，使得这两部分的面积之差最大，则该直线的方程为( )
| A．x＋y－2＝0 | B．y－1＝0 |
| C．x－y＝0 | D．x＋3y－4＝0 |
已知点A（﹣3，0），B（0，3），若点P在圆x2+y2﹣2x=0上运动，则△PAB面积的最小值为（ ）
| A．6 | B．6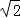 | C．6+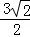 | D．6﹣ |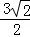
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A．(x+1)2+y2=2 | B．(x-1)2+y2=2 |
| C．(x+1)2+y2=4 | D．(x-1)2+y2=4 |