题目内容
【题目】已知函数f(x)=alnx﹣x2 , a∈R,
(1)求函数f(x)的单调区间;
(2)若x≥1时,f(x)≤0恒成立,求实数a的取值范围;
(3)设a>0,若A(x1 , y1),B(x2 , y2)为曲线y=f(x)上的两个不同点,满足0<x1<x2 , 且x3∈
(x1 , x2),使得曲线y=f(x)在x=x3处的切线与直线AB平行,求证:x3< ![]() .
.
【答案】
(1)
解:∵函数f(x)=alnx﹣x2,x>0,a∈R,
∴f′(x)= ![]() ﹣2x=
﹣2x= ![]() ;
;
当a≤0时,∵x>0,∴f′(x)<0,∴f(x)在定义域上是减函数;
当a>0时,令f′(x)=0,即a﹣2x2=0,解得x= ![]() ,
,
∴x> ![]() 时,f′(x)<0,f(x)是减函数,
时,f′(x)<0,f(x)是减函数,
0<x< ![]() 时,f′(x)>0,f(x)是增函数;
时,f′(x)>0,f(x)是增函数;
综上,a≤0时,f(x)的减区间是(0,+∞),
a>0时,f(x)的减区间是( ![]() ,+∞),增区间是(0,
,+∞),增区间是(0, ![]() );
);
(2)
解:根据(1)知,a≤0时,f(x)的减区间是(0,+∞),
令f(1)<0,则﹣x2<0恒成立,∴a≤0满足题意;
a>0时,f(x)的减区间是( ![]() ,+∞),增区间是(0,
,+∞),增区间是(0, ![]() );
);
当 ![]() ≤1,即0<a≤2时,f(x)在(1,+∞)上是减函数,∴0<a≤2满足题意;
≤1,即0<a≤2时,f(x)在(1,+∞)上是减函数,∴0<a≤2满足题意;
当 ![]() >1,即a>2时,f(x)的最大值是f(
>1,即a>2时,f(x)的最大值是f( ![]() ),令f(
),令f( ![]() )≤0,
)≤0,
即aln ![]() ﹣
﹣ ![]() ≤0,解得a≤2e,即2<a≤2e满足题意;
≤0,解得a≤2e,即2<a≤2e满足题意;
综上,a的取值范围是a≤2e;
(3)
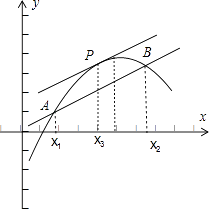
解:当a>0时,A(x1,y1),B(x2,y2)为曲线y=f(x)上的两个不同点,满足0<x1<x2时,
∴x3∈(x1,x2),使得曲线y=f(x)在x=x3处的切线与直线AB平行,如图所示;
∴kAB= ![]() =
= ![]() ,
,
又∵f′(x)= ![]() ﹣2x,
﹣2x,
∴kl=f′(x3)= ![]() ﹣2x3.
﹣2x3.
∴ ![]() =
= ![]() ﹣2x3.
﹣2x3.
∵f′(x)= ![]() ﹣2x在(0,+∞)上是减函数,
﹣2x在(0,+∞)上是减函数,
∴欲证:x3< ![]() ,即证明f′(x3)>f′(
,即证明f′(x3)>f′( ![]() ),
),
即 ![]() >
> ![]() ﹣(x1+x2),
﹣(x1+x2),
变形为 ![]() >
> ![]() ,
,
∴ln ![]() >2
>2 ![]() ,
,
∴ln ![]() >2
>2 ![]() ;
;
设 ![]() =t(t>1),
=t(t>1),
则上述不等式等价于lnt>2 ![]() ,
,
即(t+1)lnt>2(t﹣1);
构造函数g(t)=lnt+ ![]() ﹣1,
﹣1,
当t>1时,g′(t)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴g′(t)在(1,+∞)上为增函数;
∴g′(t)>g′(1)=0,
∴g(t)在t>1时是增函数,
∴g(t)>g(1)=0;
∴g(t)>0在(1,+∞)上恒成立,
即(t+1)lnt>2(t﹣1)恒成立.
∴x3< ![]() 恒成立.
恒成立.
【解析】(1)求函数f(x)的导数,利用导数来判断f(x)的增减性,从而求出单调区间;(2)根据f(x)的单调区间,求出f(x)在(1,+∞)上的最大值,令最大值小于或等于0,求出a的取值范围;(3)当a>0时,求出直线AB的斜率kAB , 由直线AB与切线平行,得出x3与x1+x2的关系式;构造函数g(t),利用函数的单调性证明不等式x3< ![]() 恒成立即可.
恒成立即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 阅读快车系列答案
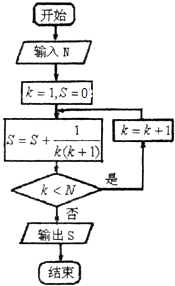
阅读快车系列答案【题目】某地区为了解70﹣80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号i | 分组 | 组中值(Gi) | 频数 | 频率(Fi) |
1 | [4,5) | 4.5 | 6 | 0.12 |
2 | [5,6) | 5.5 | 10 | 0.20 |
3 | [6,7) | 6.5 | 20 | 0.40 |
4 | [7,8) | 7.5 | 10 | 0.20 |
5 | [8,9] | 8.5 | 4 | 0.08 |
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为 .