题目内容
已知函数f(x)=4cos ωx· (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间 上的单调性.
上的单调性.
 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.(1)求ω的值;
(2)讨论f(x)在区间
 上的单调性.
上的单调性.(1)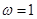 (2)
(2)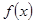 在
在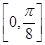 单调递增,在
单调递增,在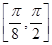 单调递减.
单调递减.
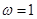 (2)
(2)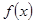 在
在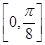 单调递增,在
单调递增,在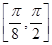 单调递减.
单调递减.试题分析:(1)利用两角和正弦公式和降幂公式化简,得到
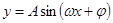 的形式,利用公式
的形式,利用公式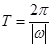 计算周期.(2)利用正弦函数的单调区间,求在
计算周期.(2)利用正弦函数的单调区间,求在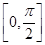 的单调性.(3)求三角函数的最小正周期一般化成
的单调性.(3)求三角函数的最小正周期一般化成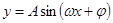 ,
,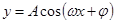 ,
,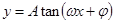 形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成
形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成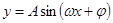 形式,再
形式,再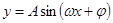 的单调区间,只需把
的单调区间,只需把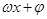 看作一个整体代入
看作一个整体代入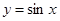 相应的单调区间,注意先把
相应的单调区间,注意先把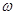 化为正数,这是容易出错的地方.
化为正数,这是容易出错的地方.试题解析:解:(1)f(x)=4cos ωx·sin
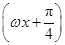
=
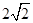 sin ωx·cos ωx+
sin ωx·cos ωx+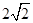 cos2ωx
cos2ωx=
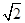 (sin 2ωx+cos 2ωx)+
(sin 2ωx+cos 2ωx)+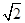
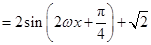 3分
3分因为f(x)的最小正周期为π,且ω>0,
从而有
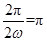 ,故ω=1. 6分
,故ω=1. 6分(2)由(1)知,f(x)=
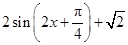 .
.若0≤x≤
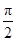 ,则
,则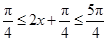 .
.当
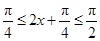 ,即
,即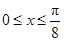 时,f(x)单调递增;
时,f(x)单调递增;当
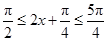 ,即
,即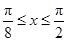 时,f(x)单调递减. 10分
时,f(x)单调递减. 10分综上可知,f(x)在区间
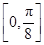 上单调递增,在区间
上单调递增,在区间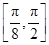 上单调递减. 12分
上单调递减. 12分
练习册系列答案
相关题目
 在一个周期内,当
在一个周期内,当 时,
时, 取得最小值
取得最小值 ;当
;当 时,
时,
 的最小正周期;
的最小正周期; 时,若
时,若 ,求
,求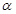 的值.
的值.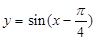 的一条对称轴可以是直线( )
的一条对称轴可以是直线( )



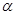 ,使
,使
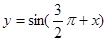 是偶函数
是偶函数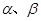 是第一象限的角,且
是第一象限的角,且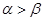 ,则
,则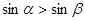 .其中正确命题的序号是________________.
.其中正确命题的序号是________________. 时,
时, 的值为 ( )
的值为 ( ) 取值有关
取值有关