题目内容
若A,B,C是△ABC的三个内角,则下列等式成立的是( )
| A.sin(B+C)=sinA | B.cos(B+C)=cosA |
| C.tan(B+C)=tanA | D.cot(B+C)=cotA |
∵A,B,C是△ABC的三个内角,
∴A+B+C=π,即B+C=π-A,
∴sin(B+C)=sin(π-A)=sinA,cos(B+C)=cos(π-A)=-cosA,tan(B+C)=tan(π-A)=-tanA,cot(B+C)=cot(π-A)=-cotA,
则等式成立的为sin(B+C)=sinC.
故选:A.
∴A+B+C=π,即B+C=π-A,
∴sin(B+C)=sin(π-A)=sinA,cos(B+C)=cos(π-A)=-cosA,tan(B+C)=tan(π-A)=-tanA,cot(B+C)=cot(π-A)=-cotA,
则等式成立的为sin(B+C)=sinC.
故选:A.

练习册系列答案
相关题目
 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 上的单调性.
上的单调性. 的图象可看成
的图象可看成 的图象按如下平移变换而得到的( ).
的图象按如下平移变换而得到的( ). 个单位
个单位 个单位
个单位 则
则 ( )
( )



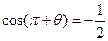 ,则
,则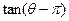 =___________________
=___________________ 的最小正周期为 ____
的最小正周期为 ____