题目内容
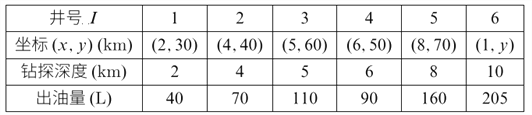
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:
(参考公式和计算结果:
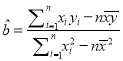 ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() 的值,并估计
的值,并估计![]() 的预报值.
的预报值.
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的![]() ,
, ![]() ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() ,
, ![]() 的预报值为24;(2)使用位置最接近的已有旧井
的预报值为24;(2)使用位置最接近的已有旧井![]() ;(3)
;(3)![]() ,分布列见解析.
,分布列见解析.
【解析】试题分析:
(1)利用前5组数据与平均数的计算公式可得![]() =5,
=5,![]() =50,代入y=6.5x+a,可得a,进而定点y的预报值.
=50,代入y=6.5x+a,可得a,进而定点y的预报值.
(2)根据计算公式可得![]() ,
, ![]() ,
, ![]() ≈10.25,
≈10.25, ![]() =5.25,
=5.25, ![]() =10.25,计算可得并且判断出结论.
=10.25,计算可得并且判断出结论.
(3)由题意,1、3、5、6这4口井是优质井,2,4这两口井是非优质井,勘察优质井数X的可能取值为2,3,4,P(X=k)=![]() ,可得X的分布列及其数学期望.
,可得X的分布列及其数学期望.
解:
(1)因为![]() ,
, ![]() .
.
回归直线必过样本中心点![]() ,则
,则![]() .
.
故回归直线方程为![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]() 的预报值为24.
的预报值为24.
(2)因为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以
![]() ,
,
![]() ,即
,即![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,均不超过10%,因此使用位置最接近的已有旧井
,均不超过10%,因此使用位置最接近的已有旧井![]() .
.
(3)由题意,1,3,5,6这4口井是优质井,2,4这两口井是非优质井,
所以勘察优质井数![]() 的可能取值为2,3,4,
的可能取值为2,3,4,
![]() ,
, ![]() ,
,
![]() .
.
X | 2 | 3 | 4 |
P |
|
|
|
![]()

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案