题目内容
9.函数f(x)=log3x+x-3零点所在大致区间是( )| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
分析 由已知条件分别求出f(1),f(2),f(3),f(4),f(5),由此利用零点存在性定理能求出结果.
解答 解:∵f(x)=log3x+x-3,
∴f(1)=log31+1-3=-2,
f(2)=log32+2-3=log32-1<0,
f(3)=log33+3-3=1,
f(4)=log34+4-3=log34+1>0,
f(5)=log35+5-3=log35+2>0,
∴函数f(x)=log3x+x-3零点所在大致区间是(2,3).
故选:B.
点评 本题考查函数的零点所在大致区间的判断,是基础题,解题时要认真审题,注意函数性质和零点存在性定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.对于任意两个实数a,b定义运算“*”如下:a*b=$\left\{\begin{array}{l}{a(a≤b)}\\{b(a>b)}\end{array}\right.$,则函数f(x)=x2*[(6-x)*(2x+15)]的最大值为( )
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
1.已知tanα=2(α∈(0,π)),则cos($\frac{5π}{2}$+2α)=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
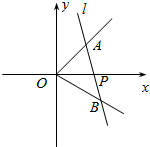 如图,射线OA、OB分别与x轴成45°角和30°角,过点P(1,0)作直线AB分别与OA、OB交于A、B.
如图,射线OA、OB分别与x轴成45°角和30°角,过点P(1,0)作直线AB分别与OA、OB交于A、B.