题目内容
【题目】(1)设椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 与双曲线
与双曲线![]() 的公共点,且△
的公共点,且△![]() 的周长为6,求椭圆
的周长为6,求椭圆![]() 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆![]() ”的方程为
”的方程为![]() ,设“盾圆
,设“盾圆![]() ”上的任意一点
”上的任意一点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求证:
,求证:![]() 为定值;
为定值;
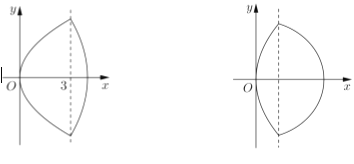
(3)由抛物线弧![]() (
(![]() )与第(1)小题椭圆弧
)与第(1)小题椭圆弧![]()
![]() (
(![]() )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆![]() ”,设过点
”,设过点![]() 的直线与“盾圆
的直线与“盾圆![]() ”交于
”交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() (
(![]() ),试用
),试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() .
.
【解析】
(1)由由![]() 的周长为
的周长为![]() 得
得![]() ,由椭圆
,由椭圆![]() 与双曲线共焦点可得
与双曲线共焦点可得![]() 值,根据平方关系求得
值,根据平方关系求得![]() ,进而即可得到椭圆方程;
,进而即可得到椭圆方程;
(2)设“盾圆![]() ”上的任意一点
”上的任意一点![]() 的坐标为
的坐标为![]() ,
,![]() ,分为
,分为![]() 与
与![]() 两种情况表示出
两种情况表示出![]() ,再分别计算
,再分别计算![]() ,即可求得定值;
,即可求得定值;
(3)由“盾圆![]() ”的对称性,不妨设
”的对称性,不妨设![]() 在
在![]() 轴上方(或
轴上方(或![]() 轴上),分类讨论:
轴上),分类讨论:![]() 时,
时,![]() 在椭圆弧
在椭圆弧![]() 上;
上;![]() 时,
时,![]() 在抛物弧
在抛物弧![]() 上,由条件可表示出此时
上,由条件可表示出此时![]() ,相应地,
,相应地, ![]() 再按
再按![]() 时,
时, ![]() 在抛物弧
在抛物弧![]() 上,
上,![]() 在椭圆弧
在椭圆弧![]() 上;当
上;当![]() 时,
时,![]() 在椭圆弧
在椭圆弧![]() 上,
上, ![]() 在抛物弧
在抛物弧![]() 上;当
上;当![]() 时,
时, ![]() 、
、![]() 在椭圆弧
在椭圆弧![]() 上,利用三角函数性质分别求出
上,利用三角函数性质分别求出![]() 的范围
的范围
(1)由![]() 的周长为
的周长为![]() 得
得![]() ,椭圆
,椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点,所以
有相同的焦点,所以![]() ,即
,即![]() ,则
,则![]() ,
,![]() ,则椭圆
,则椭圆![]() 的方程为
的方程为![]()
(2)证明:设“盾圆![]() ”上的任意一点
”上的任意一点![]() 的坐标为
的坐标为![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() ,
,
即![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
即![]() ;
;
所以![]() 为定值.
为定值.
(3)显然“盾圆![]() ”由两部分合成,所以按
”由两部分合成,所以按![]() 在抛物弧
在抛物弧![]() 或椭圆弧
或椭圆弧![]() 上加以分类,由“盾圆
上加以分类,由“盾圆![]() ”的对称性,不妨设
”的对称性,不妨设![]() 在
在![]() 轴上方(或
轴上方(或![]() 轴上);
轴上);
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ;
;
当![]() 时,
时,![]() 在椭圆弧
在椭圆弧![]() 上,由题设知
上,由题设知![]() 代入
代入![]() 得,
得,![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
当![]() 时,
时,![]() 在抛物弧
在抛物弧![]() 上,方程或定义均可得到
上,方程或定义均可得到![]() ,于是
,于是![]() ,
,
综上,![]() 或
或![]()
![]() ;
;
相应地,![]() ,
,
当![]() 时,
时, ![]() 在抛物弧
在抛物弧![]() 上,
上,![]() 在椭圆弧
在椭圆弧![]() 上,
上,
![]() ;
;
当![]() 时,
时,![]() 在椭圆弧
在椭圆弧![]() 上,
上, ![]() 在抛物弧
在抛物弧![]() 上,
上,
![]() ;
;
当![]() 时,
时, ![]() 、
、![]() 在椭圆弧
在椭圆弧![]() 上,
上,
![]() ;
;
综上, ![]() ,
,![]() ;
;![]() ,
,![]() ;
;
![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目