题目内容
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() ;
;
(2)若![]() 在线段
在线段![]() 上,且
上,且![]() ,能否在棱
,能否在棱![]() 上找到一点
上找到一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求四面体
?若存在,求四面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接PF,BD由三线合一可得AD⊥BF,AD⊥PF,故而AD⊥平面PBF,于是AD⊥PB;
(2)先证明PF⊥平面ABCD,再作PF的平行线,根据相似找到G,再利用等积转化求体积.
连接PF,BD,
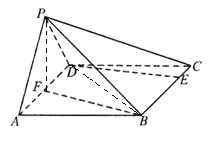
∵![]() 是等边三角形,F为AD的中点,
是等边三角形,F为AD的中点,
∴PF⊥AD,
∵底面ABCD是菱形,![]() ,
,
∴△ABD是等边三角形,∵F为AD的中点,
∴BF⊥AD,
又PF,BF平面PBF,PF∩BF=F,
∴AD⊥平面PBF,∵PB平面PBF,
∴AD⊥PB.
(2)由(1)得BF⊥AD,又∵PD⊥BF,AD,PD平面PAD,
∴BF⊥平面PAD,又BF平面ABCD,
∴平面PAD⊥平面ABCD,
由(1)得PF⊥AD,平面PAD∩平面ABCD=AD,
∴PF⊥平面ABCD,
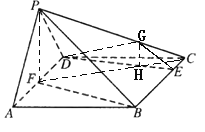
连接FC交DE于H,则△HEC与△HDF相似,又![]() ,∴CH=
,∴CH=![]() CF,
CF,
∴在△PFC中,过H作GH![]() PF交PC于G,则GH⊥平面ABCD,又GH
PF交PC于G,则GH⊥平面ABCD,又GH![]() 面GED,则面GED⊥平面ABCD,
面GED,则面GED⊥平面ABCD,
此时CG=![]() CP,
CP,
∴四面体![]() 的体积
的体积![]() .
.
所以存在G满足CG=![]() CP, 使平面
CP, 使平面![]() 平面
平面![]() ,且
,且![]() .
.

【题目】为了比较注射![]() ,
,![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .下表1和表2分别是注射药物
.下表1和表2分别是注射药物![]() 和药物
和药物![]() 后的实验结果.(疱疹面积单位:
后的实验结果.(疱疹面积单位:![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
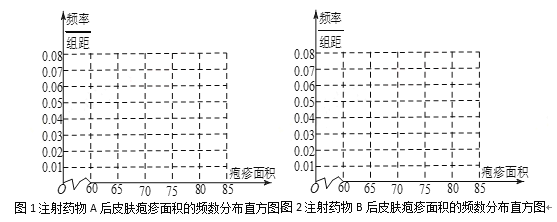
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(2)完成下面![]() 列联表,并回答能否有99.9%的把握认为“注射药物
列联表,并回答能否有99.9%的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物 | |||
注射药物 | |||
合计 |
附: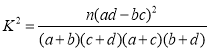
| 0.100 | 0.050 | 0.025 | 0.01 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
