题目内容
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶ | B.1∶9 | C.1∶ | D.1∶ |
D
解析试题分析:设小锥体的高为h1,大锥体的高为h2,利用一个锥体被平行于底面的截面所截得的小锥体与原锥体体积之比等于相似比的立方,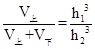
而这个截面面积与底面面积之比等于相似比的平方,即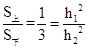 可得
可得 ,进而得到体积的比,为D.
,进而得到体积的比,为D.
考点:本题主要考查了几何体的体积比与相似比的关系,常用此法简化解题过程,同学注意掌握应用.
点评:解决该试题的关键是几何体中,体积比是相似比的立方,面积比是相似比的平方,直接求解即可得到结论。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
某四棱锥的三视图如图所示,该四棱锥的表面积是 ( )
| A.32 | B.16+ | C.48 | D. |
右图是某四棱锥的三视图,则该几何体的表面积等于 ( )
A. | B. | C. | D. |
正方体的内切球的体积为 , 则此正方体的表面积是
, 则此正方体的表面积是
| A.216 | B.72 | C.108 | D.648 |
下列说法错误的是( )
| A.棱柱的两个底面互相平行 | B.圆台与棱台统称为台体 |
| C.棱柱的侧棱垂直于底面 | D.圆锥的轴截面是一个等腰三角形 |
在正方体 中,
中, 分别为
分别为 ,
, ,
, ,
, 的中点,则异面直线
的中点,则异面直线 与
与 所成的角等于( )
所成的角等于( )
A. | B.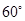 | C. | D.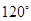 |
某几何体的三视图如右图,其正视图中的曲线部分为半个圆弧,则该几何体的体积为( )

A. | B. | C. | D. |



 B.
B. C.
C.  D.
D.