题目内容
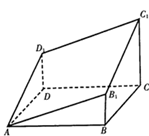
某四棱锥的三视图如图所示,该四棱锥的表面积是 ( )
| A.32 | B.16+ | C.48 | D. |
B
解析试题分析:由题意知原几何体是正四棱锥,其中正四棱锥的高为2,底面是一个边长为4的正方形,过顶点向底面做垂线,垂线段长是2,过底面的中心向长度是4的边做垂线,连接垂足与顶点,得到直角三角形,得到斜高是2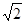 ,所以四个侧面积是
,所以四个侧面积是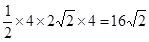 ,底面面积为
,底面面积为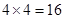 ,所以该四棱锥的表面积是16+
,所以该四棱锥的表面积是16+ 。故选B.
。故选B.
考点:三视图;棱锥的体积公式。
点评:本题考查由三视图求几何体的表面积,做此题型的关键是正确还原几何体及几何体的棱的长度。

练习册系列答案
相关题目
(理)球O与锐二面角α-l-β的两半平面相切,两切点间的距离为,O点到交线l的距离为2,则球O的表面积为( )
| A. | B.4π | C.12π | D.36π |
圆锥母线长为1,侧面展开图的圆心角为240°,则圆锥体积为( )
A. | B. | C. | D. |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.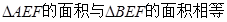 |
若某空间几何体的三视图如图所示,则该几何体的体积是( )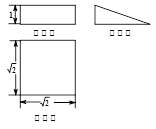
A. | B.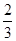 | C.1 | D. 2 |
若三棱锥的一条棱长为 ,其余棱长均为1,体积是
,其余棱长均为1,体积是 ,则函数
,则函数 在其定义域上为( )
在其定义域上为( )
| A.增函数且有最大值 | B.增函数且没有最大值 |
| C.不是增函数且有最大值 | D.不是增函数且没有最大值 |
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶ | B.1∶9 | C.1∶ | D.1∶ |