Question

长方体ABCD—A₁B₁C₁D₁中，AA₁=AB=2，AD=1， 点E、F、G分别是DD₁、AB、CC₁的中点，则异面直线A₁E与GF所成的角是（   ）

A.           B.          C.           D.

Answer 1

D

解析试题分析：连接B₁G，则,所以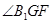就是异面直线A₁E与GF所成的角，连接B₁F，
在中，,所以,
所以.
考点：长方体的性质，异面直线所成的角.
点评：找或做出异面直线所成的角，根据异面直线所成的角的定义要转化为求两条相交直线所成的角来解决.