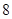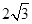题目内容
正方体的内切球的体积为
, 则此正方体的表面积是
| A．216 | B．72 | C．108 | D．648 |
A
解析试题分析：设正方体的棱长为a，则正方体内切球的半径为
，所以
，即a=6，所以正方体的表面积是216.
考点：本题考查空间几何体的体积、表面积公式。
点评：本题考查的知识点是正方体的体积，球的体积，其中根据正方体的内切球直径等于正方体的棱长，求出球的半径，是解答本题的关键。
练习册系列答案
孟建平名校考卷系列答案
相关题目
如图，正方体
的棱长为1，线段
上有两个动点E，F，且
，则下列结论中错误的是 （ ）
A． |
B． |
C．三棱锥 的体积为定值 |
D． |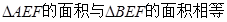
若三棱锥的一条棱长为
，其余棱长均为1，体积是
，则函数在其定义域上为（ ）
| A．增函数且有最大值 | B．增函数且没有最大值 |
| C．不是增函数且有最大值 | D．不是增函数且没有最大值 |
如图，在正方体
中，
为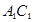
的中点，则异面直线
与
所成的角为( )
| A．30° | B．45° | C．60° | D．90 ° |
正方体
，棱长为
，点
到截面
的距离为( )
A． | B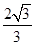． | C． | D． |
在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为（ ）
A．1∶ | B．1∶9 | C．1∶ | D．1∶ |
，一个内角为
的菱形，俯视图为正方形，那么这个几何体的表面积为
