题目内容
已知双曲线
-y2=1的左、右顶点分别为A1、A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
| x2 | 2 |
分析:由直线的斜率公式与直线的点斜式方程,求出直线A1P、A2Q方程分别为y=
(x+
)、y=
(x-
).将两条直线方程的左右两边对应相乘,并利用点P(x1,y1)在双曲线
-y2=1上对所得的式子化简,整理得
+y2=1,即为轨迹E的方程,再对所求的轨迹加以检验即可得到答案.
| y1 | ||
x1+
|
| 2 |
| -y1 | ||
x1-
|
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
解答:解:由题设知|x1|>
,A1(-
,0),A2(
,0),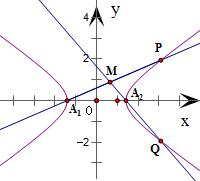
∵直线A1P的斜率为k1=
,
∴直线A1P的方程为y=
(x+
),…①
同理可得直线A2Q的方程为y=
(x-
).…②
将①②两式相乘,得y2=
(x2-2).…③
∵点P(x1,y1)在双曲线
-y2=1上,
∴
-y12=1,可得y12=
-1=
(x12-2),…④
将④代入③,得y2=
(x2-2)=
x2-1,整理得
+y2=1,即为轨迹E的方程.
∵点P、Q不重合,且它们不与A1、A2重合,
∴x≠0且x≠±
,轨迹E的方程为
+y2=1(x≠0且x≠±
)
| 2 |
| 2 |
| 2 |

∵直线A1P的斜率为k1=
| y1 | ||
x1+
|
∴直线A1P的方程为y=
| y1 | ||
x1+
|
| 2 |
同理可得直线A2Q的方程为y=
| -y1 | ||
x1-
|
| 2 |
将①②两式相乘,得y2=
| y12 |
| 2-x12 |
∵点P(x1,y1)在双曲线
| x2 |
| 2 |
∴
| x12 |
| 2 |
| x12 |
| 2 |
| 1 |
| 2 |
将④代入③,得y2=
| ||
| 2-x12 |
| 1 |
| 2 |
| x2 |
| 2 |
∵点P、Q不重合,且它们不与A1、A2重合,
∴x≠0且x≠±
| 2 |
| x2 |
| 2 |
| 2 |
点评:本题给出双曲线上两条动直线,求直线的交点轨迹方程.着重考查了双曲线的标准方程、直线的基本量与基本形式和动点轨迹的求法等知识,属于中档题.

练习册系列答案
相关题目