题目内容
已知双曲线| x2 | 2 |
(1)求直线l的方程;
(2)若点M在直线l与x≥0,y≥0所围成的三角形的三条边上及三角形内运动,求z=-x+y的最小值.
分析:本题考查的知识点是直线的一般式方程,及简单的线性规划,(1)由过点P(0,1)作斜率k<0的直线l与双曲线
-y2=1恰有一个交点.联立直线与双曲线的方程,则易得到直线的斜率,代入即可得到直线的方程.(2)我们画出直线l与x≥0,y≥0所围成的三角形,求出三角形的各个顶点,代入即可得到目标函数z=-x+y的最小值.
| x2 |
| 2 |
解答:解:(1)由于直线l过P(0,1)点,
设直线l的方程为:y=kx+1(k<0)
将直线方程代入双曲线方程
-y2=1得:
(
-k2)x2-2kx-2=0①
由直线l与双曲线恰有一个交点,则方程①的△=0
即4k2+8(
-k2)=0
解得k=-1
∴直线l的方程为:y=-x+1
即:x+y-1=0
(2)直线l与x≥0,y≥0所围成的三角形如下图示:
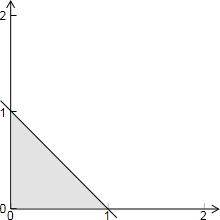
由图可知:当经x=1,y=0时,目标函数z=-x+y有最小值-1
设直线l的方程为:y=kx+1(k<0)
将直线方程代入双曲线方程
| x2 |
| 2 |
(
| 1 |
| 2 |
由直线l与双曲线恰有一个交点,则方程①的△=0
即4k2+8(
| 1 |
| 2 |
解得k=-1
∴直线l的方程为:y=-x+1
即:x+y-1=0
(2)直线l与x≥0,y≥0所围成的三角形如下图示:

由图可知:当经x=1,y=0时,目标函数z=-x+y有最小值-1
点评:在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.

练习册系列答案
相关题目