题目内容
(本小题满分12分)
用数学归纳法证明: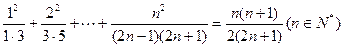 。
。
用数学归纳法证明:
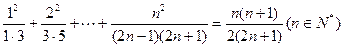 。
。见解析
证明(1)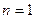 时,
时,
左边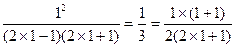 =右边,等式成立…………3分
=右边,等式成立…………3分
(2)假设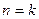 时等式成立,
时等式成立,
即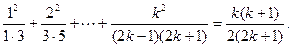 ………………4分
………………4分
则
左边=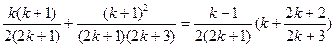 …………6分
…………6分
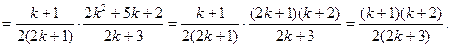 ………10分
………10分
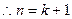 时,等式成立
时,等式成立
由(1)(2)知,对一切
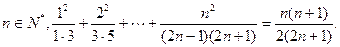 …………12分
…………12分
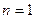 时,
时,左边
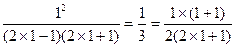 =右边,等式成立…………3分
=右边,等式成立…………3分(2)假设
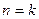 时等式成立,
时等式成立,即
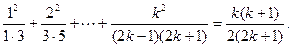 ………………4分
………………4分则

左边=
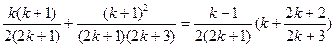 …………6分
…………6分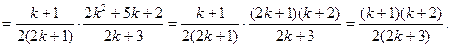 ………10分
………10分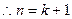 时,等式成立
时,等式成立由(1)(2)知,对一切
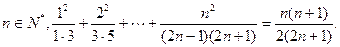 …………12分
…………12分
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
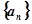 的前
的前 项和为
项和为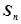 ,满足
,满足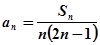 ,且
,且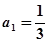 .
.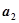 ,
,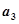 ,
,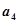 ;
; 对于一切
对于一切 都成立?
都成立? 为常数,且
为常数,且

 有
有 ,求
,求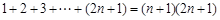 时,当
时,当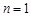 时左边表达式是 ;从
时左边表达式是 ;从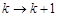 需增添的项的是 .
需增添的项的是 . 成立,起始值至少应取为( )
成立,起始值至少应取为( )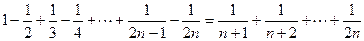 ”时,
”时,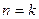 的假设证明
的假设证明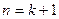 时,如果从等式左边证明右边,则必须证得右边为( )
时,如果从等式左边证明右边,则必须证得右边为( ) 、
、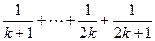 B、
B、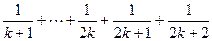

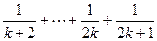 D、
D、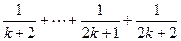
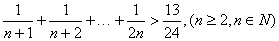 ”的过程中,
”的过程中,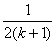
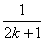 和
和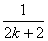

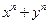 能被
能被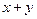 整除”,在第二步时,正确的证法是( )
整除”,在第二步时,正确的证法是( )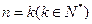 ,证明
,证明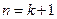 命题成立
命题成立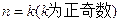 ,证明
,证明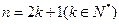 ,证明
,证明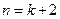 命题成立
命题成立