题目内容
【题目】随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯，由此催生了一批外卖点餐平台．已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取100名点外卖的用户进行统计，按送餐距离分类统计结果如表：
送餐距离（千米） | （0，1] | （1，2] | （2，3] | （3，4] | （4，5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率．
（1）若某送餐员一天送餐的总距离为100千米，试估计该送餐员一天的送餐份数；（四舍五入精确到整数，且同一组中的数据用该组区间的中点值为代表）．
（2）若该外卖平台给送餐员的送餐费用与送餐距离有关，规定2千米内为短距离，每份3元，2千米到4千米为中距离，每份7元，超过4千米为远距离，每份12元．记X为送餐员送一份外卖的收入（单位：元），求X的分布列和数学期望．
【答案】（1）41份（2）见解析，6.15
【解析】
（1）利用频率分布表，计算每名外卖用户的平均送餐距离．然后求解送餐份数．
（2）由题意知X的可能取值为：3，7，12，求出概率，得到分布列，然后求解期望即可．
解：（1）估计每名外卖用户的平均送餐距离为：0.5×0.15+1.5×0.25+2.5×0.25+3.5×0.2+4.5×0.15＝2.45千米．
所以送餐距离为100千米时，送餐份数为：
份；
（2）由题意知X的可能取值为：3，7，12，
，
，
，
所以X的分布列为：
X | 3 | 7 | 12 |
P |
|
|
|
∴
．
【题目】下表为2016年至2019年某百货零售企业的线下销售额（单位：万元），其中年份代码
年份
．
年份代码 | 1 | 2 | 3 | 4 |
线下销售额 | 95 | 165 | 230 | 310 |
（1）已知
与
具有线性相关关系，求关于的线性回归方程，并预测2020年该百货零售企业的线下销售额；
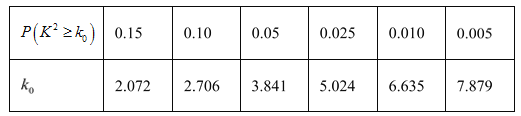
（2）随着网络购物的飞速发展，有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑，某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法，随机调查了55位男顾客、50位女顾客（每位顾客从“持乐观态度”和“持不乐观态度”中任选一种），其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人，能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关？
参考公式及数据：
．
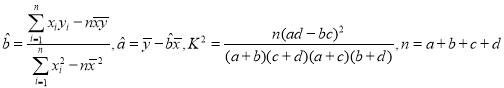