题目内容
3.若函数f(x)=sin(ωx+θ)的图象(部分)如图所示,则ω和θ的取值是( )
| A. | $ω=1,θ=\frac{π}{3}$ | B. | $ω=1,θ=-\frac{π}{3}$ | C. | $ω=\frac{1}{2},θ=\frac{π}{6}$ | D. | $ω=\frac{1}{2},θ=-\frac{π}{6}$ |
分析 由函数图象可得:T=$\frac{2π}{ω}$=4($\frac{2π}{3}$+$\frac{π}{3}$),解得ω的值,由于点(-$\frac{π}{3}$,0)在函数图象上,可得:sin[$\frac{1}{2}×(-\frac{π}{3})+θ$]=0,解得θ的值,从而得解.
解答 解:由函数图象可得:T=$\frac{2π}{ω}$=4($\frac{2π}{3}$+$\frac{π}{3}$),解得$ω=\frac{1}{2}$,
由于点(-$\frac{π}{3}$,0)在函数图象上,可得:sin[$\frac{1}{2}×(-\frac{π}{3})+θ$]=0,解得:θ=kπ+$\frac{π}{6}$,k∈Z
当k=0时,可得$θ=\frac{π}{6}$,
故选:C.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,属于基本知识的考查.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11.已知函数y=f(-|x|)的图象如左图所示,则函数y=f(x)的图象不可能是( )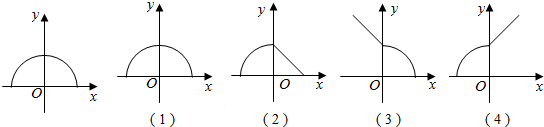
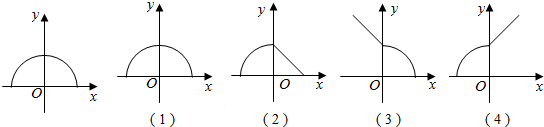
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
8.曲线$y=\frac{x}{x-2}$在点(1,-1)处的切线方程是( )
| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x+1 | D. | y=-2x-2 |
15.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | y=|x-1| | B. | y=-x2 | C. | $y=\sqrt{x+1}$ | D. | y=2-x |