题目内容
17.如果直角三角形周长为2,则它的最大面积为$3-2\sqrt{2}$.分析 设直角三角形的两直角边为a、b,利用勾股定理求出斜边c的表达式,由周长和基本不等式求出ab的范围,根据三角形的面积即可求出直角三角形面积的最大值.
解答 解:设直角三角形的两直角边分别为a、b,则斜边c=$\sqrt{{a}^{2}+{b}^{2}}$,
由已知得a+b+c=2,∴a+b+$\sqrt{{a}^{2}+{b}^{2}}$=2,
∵a+b+$\sqrt{{a}^{2}+{b}^{2}}$≥2$\sqrt{ab}$+$\sqrt{2}$$\sqrt{ab}$(当且仅当a=b时取等号),
∴2≥(2+$\sqrt{2}$)$\sqrt{ab}$,解得$\sqrt{ab}$≤$\frac{2}{2+\sqrt{2}}$=2-$\sqrt{2}$,
则ab≤6-4$\sqrt{2}$,
∴直角三角形的面积S=$\frac{1}{2}ab$≤$3-2\sqrt{2}$,
∴直角三角形面积的最大值是$3-2\sqrt{2}$,
故答案为:$3-2\sqrt{2}$.
点评 本题考查了基本不等式的实际应用,列出有关量的函数关系式或方程式是解题关键,注意基本不等式的三个条件,属于基础题.

练习册系列答案
相关题目
8.曲线$y=\frac{x}{x-2}$在点(1,-1)处的切线方程是( )
| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x+1 | D. | y=-2x-2 |
9.复数m2+2m-3+(m-1)i(m∈R)为纯虚数,则( )
| A. | m=1,m=-3 | B. | m=1 | C. | m=-3 | D. | m=3 |
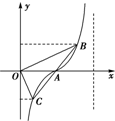 函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )
函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )