题目内容
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.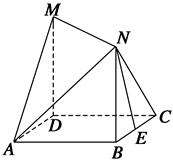
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.

解:(1)在如图,以D为坐标原点,建立空间直角坐标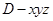
依题意,得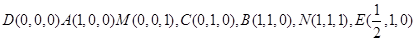 。
。
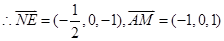
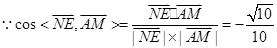 ,…………5分
,…………5分
所以异面直线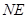 与
与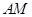 所成角的余弦值为
所成角的余弦值为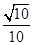 …………6分
…………6分
(2)假设在线段 上存在点
上存在点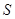 ,使得
,使得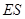
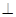 平面
平面 .
.
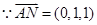 ,可设
,可设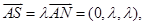
又 ……….8 分
……….8 分
由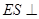 平面
平面 ,得
,得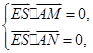 即
即
故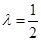 ,此时
,此时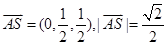 .………………10分
.………………10分
经检验,当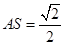 时,
时,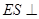 平面
平面 .
.
故线段 上存在点
上存在点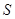 ,使得
,使得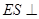 平面
平面 ,此时
,此时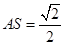 …………13分
…………13分
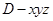
依题意,得
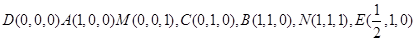 。
。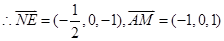
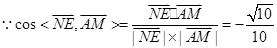 ,…………5分
,…………5分所以异面直线
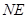 与
与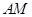 所成角的余弦值为
所成角的余弦值为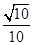 …………6分
…………6分(2)假设在线段
 上存在点
上存在点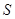 ,使得
,使得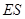
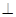 平面
平面 .
.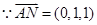 ,可设
,可设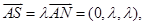
又
 ……….8 分
……….8 分由
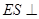 平面
平面 ,得
,得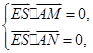 即
即
故
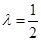 ,此时
,此时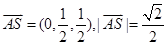 .………………10分
.………………10分经检验,当
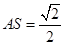 时,
时,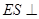 平面
平面 .
.故线段
 上存在点
上存在点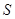 ,使得
,使得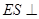 平面
平面 ,此时
,此时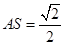 …………13分
…………13分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
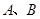 为空间的两个不同的点,且
为空间的两个不同的点,且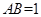 ,空间中适合条件
,空间中适合条件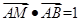 的点
的点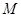 的集合表示的图形是 .
的集合表示的图形是 . 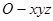 中,点
中,点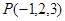 关于
关于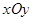 平面的对称点坐标为
平面的对称点坐标为 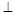 平面ABC,AE
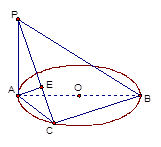
平面ABC,AE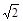 .
.
 、
、 、
、 为两两垂直的单位向量,非零向量
为两两垂直的单位向量,非零向量 ,若向量
,若向量 与向量
与向量 、
、 、
、 ,则
,则 .
.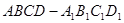 中,
中,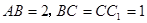 ,
,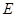 为棱
为棱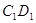 的中点.
的中点.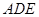
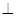 面
面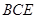 ;
;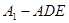 的体积
的体积
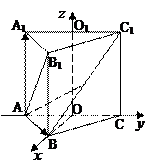
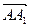 、
、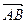 、
、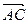 表示向量
表示向量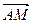 ;
;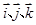 为空间两两垂直的单位向量,且
为空间两两垂直的单位向量,且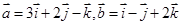 ,则
,则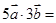 ( )
( )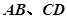 互相垂直,且
互相垂直,且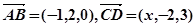 ,则
,则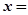 ( )
( )