题目内容
在长方体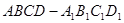 中,
中,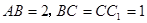 ,
,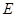 为棱
为棱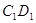 的中点.
的中点.
(Ⅰ)求证面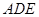
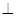 面
面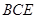 ;
;
(Ⅱ)求三棱锥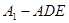 的体积
的体积

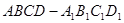 中,
中,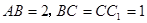 ,
,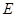 为棱
为棱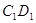 的中点.
的中点.(Ⅰ)求证面
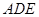
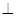 面
面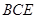 ;
;(Ⅱ)求三棱锥
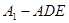 的体积
的体积
(1)
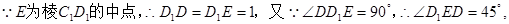
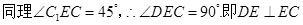
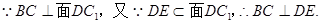 …………………………2分
…………………………2分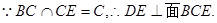 …………………………4分
…………………………4分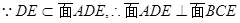 ………………6分
………………6分(2)三棱锥
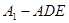 可以看做以面
可以看做以面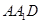 为底
为底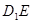 为高的三棱锥,
为高的三棱锥,
略

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
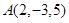 关于xOy面的对称点,则
关于xOy面的对称点,则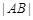 =
= 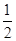
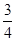
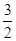
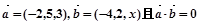 ,则
,则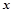 =( )
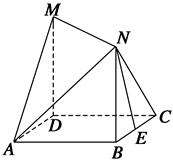
=( ) 的顶点D为坐标原点O,建立如图空间直角坐标系,则与
的顶点D为坐标原点O,建立如图空间直角坐标系,则与 共线的向量的坐标可以是( )
共线的向量的坐标可以是( )



