题目内容
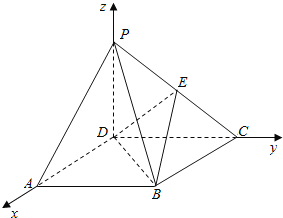
【题目】如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.

(Ⅰ)证明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
(Ⅰ)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,利用向量法能证明PA∥平面BDE;(Ⅱ)由已知求出平面BDE的一个法向量和平面DEC的一个法向量,利用向量法能求出二面角B﹣DE﹣C的余弦值;(Ⅲ)由已知得PB⊥DE,假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=
,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.
(Ⅰ)证明:以D为坐标原点,
分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0),
![]() =(2,0,﹣2),
=(2,0,﹣2),![]() =(0,1,1),
=(0,1,1),![]() ,
,
设![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由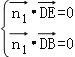 ,得
,得![]() ,
,
取y=﹣1,得![]() .
.
∵![]() =2﹣2=0,∴
=2﹣2=0,∴![]() ,
,
又PA不包含于平面BDE,PA∥平面BDE;
(Ⅱ)由(Ⅰ)知![]() =(1,﹣1,1)是平面BDE的一个法向量,
=(1,﹣1,1)是平面BDE的一个法向量,
又![]() =
=![]() =(2,0,0)是平面DEC的一个法向量.
=(2,0,0)是平面DEC的一个法向量.
设二面角B﹣DE﹣C的平面角为θ,
∴cosθ=cos<![]() ,
,![]() >=
>=![]() .
.
故二面角B﹣DE﹣C的余弦值为![]() .
.
(Ⅲ)∵![]() =(2,2,﹣2),
=(2,2,﹣2),![]() =(0,1,1),
=(0,1,1),
∴![]() =0,∴PB⊥DE,
=0,∴PB⊥DE,
假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),
,(0<λ∠1),
则![]() =(2λ,2λ,﹣2λ),
=(2λ,2λ,﹣2λ),![]() =
=![]() =(2λ,2λ,2﹣2λ),
=(2λ,2λ,2﹣2λ),
由![]() =0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
=0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
∴![]() ∈(0,1),此时PF=
∈(0,1),此时PF=![]() ,
,
即在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.

 阅读快车系列答案
阅读快车系列答案【题目】某学校为了调查高一年级学生的体育锻炼情况,从甲、乙、丙3个班中,按分层抽样的方法获得了部分学生一周的锻炼时间(单位:h),数据如下,
甲 | 6 | 6.5 | 7 | 7.5 | 8 | |||
乙 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
丙 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | 12 | 13.5 |
(1)求三个班中学生人数之比;
(2)估计这个学校高一年级学生中,一周的锻炼时间超过10h的百分比;
(3)估计这个学校高一年级学生一周的平均锻炼时间.
