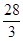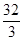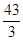题目内容
如果方程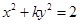 表示焦点在y轴上的椭圆,则实数k的取值范围是( )
表示焦点在y轴上的椭圆,则实数k的取值范围是( )
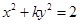 表示焦点在y轴上的椭圆,则实数k的取值范围是( )
表示焦点在y轴上的椭圆,则实数k的取值范围是( )| A.(0,+∞) | B.(0,2) | C.(1,+∞) | D.(0,1) |
D
试题分析:方程
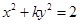 化为标准形式
化为标准形式 ,焦点在y轴上,所以
,焦点在y轴上,所以
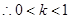
点评:椭圆的焦点位置的判定方法:将方程整理为标准方程,看
 对应的分母哪个更大些,焦点就在哪个轴上
对应的分母哪个更大些,焦点就在哪个轴上
练习册系列答案
相关题目
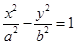 的一个焦点与抛物线
的一个焦点与抛物线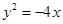 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为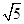 ,则此双曲线的方程为
,则此双曲线的方程为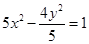
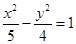
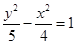
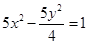
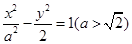 的两条渐近线的夹角为
的两条渐近线的夹角为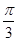 ,则双曲线的离心率为( )
,则双曲线的离心率为( )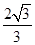
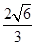
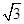
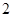
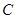 :
: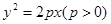 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.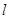 与抛物线
与抛物线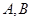 ,若满足
,若满足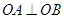 ,证明直线
,证明直线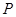 的坐标.
的坐标.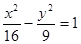 的右顶点为焦点的抛物线的标准方程为 ( )
的右顶点为焦点的抛物线的标准方程为 ( )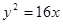
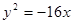

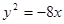
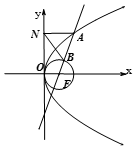
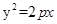 (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心,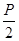 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠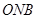 = .
= .
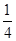



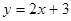 与抛物线
与抛物线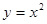 所围成的图形面积是( )
所围成的图形面积是( )