题目内容
【题目】已知数列{an}满足a2= ![]() ,且an+1=3an﹣1(n∈N*).
,且an+1=3an﹣1(n∈N*).
(1)求数列{an}的通项公式以及数列{an}的前n项和Sn的表达式;
(2)若不等式 ![]() ≤m对n∈N*恒成立,求实数m的取值范围.
≤m对n∈N*恒成立,求实数m的取值范围.
【答案】
(1)解:∵an+1=3an﹣1(n∈N*),∴an+1﹣ ![]() =3(an﹣
=3(an﹣ ![]() ),
),
∴数列 ![]() 是等比数列,首项为3,公比为3.
是等比数列,首项为3,公比为3.
∴an﹣ ![]() =3×3n﹣1=3n,
=3×3n﹣1=3n,
∴an= ![]() +3n,
+3n,
∴Sn= ![]() +
+ ![]() =
= ![]()
(2)解:不等式 ![]() ≤m,化为:
≤m,化为: ![]() ≤m,
≤m,
∵ ![]() =
= ![]() 单调递减,
单调递减,
∴m≥ ![]() =
= ![]() .
.
∴实数m的取值范围是 ![]()
【解析】(1)由an+1=3an﹣1(n∈N*),可得an+1﹣ ![]() =3(an﹣
=3(an﹣ ![]() ),利用等比数列的通项公式与求和公式即可得出.(2)不等式
),利用等比数列的通项公式与求和公式即可得出.(2)不等式 ![]() ≤m,化为:
≤m,化为: ![]() ≤m,由于
≤m,由于 ![]() =
= ![]() 单调递减,即可得出m的求值范围.
单调递减,即可得出m的求值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系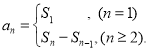 .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程 ![]() =
= ![]() t+
t+ ![]() .
.
(Ⅱ)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() =
= ![]() t+
t+ ![]() 中
中 .
.