题目内容
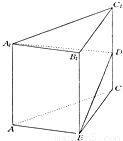 如图,已知直三棱柱ABC-A1B1C1,侧棱长为2,底面△ABC中,∠B=90°,AB=1,BC=
如图,已知直三棱柱ABC-A1B1C1,侧棱长为2,底面△ABC中,∠B=90°,AB=1,BC=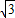 ,D是侧棱CC1上一点,且BD与底面所成角为30°.
,D是侧棱CC1上一点,且BD与底面所成角为30°.(1)求点D到AB所在直线的距离.
(2)求二面角A1-BD-B1的度数.
【答案】分析:(1)根据线面垂直的性质可知AB⊥BD即BD为点D到AB所在直线的距离,再根据线面所成角的定义可知∠DBC即为BD与底面所成角,可求出BD,即可求得所求;
(2)过B1作BD的垂线角BD与E,连接A1E,B1E,根据二面角平面角的定义可知∠A1EB1为二面角A1-BD-B1的平面角,在直角三角形A1B1E中,求出此角即可.
解答: 解:(1)∵BD在底面的射影为BC
解:(1)∵BD在底面的射影为BC
∴∠DBC即为BD与底面所成角则∠DBC=30°
∵∠B=90°,直三棱柱ABC-A1B1C1,
∴AB⊥侧面BC1,而BD?侧面BC1,
∴AB⊥BD即BD为点D到AB所在直线的距离
在直角三角形BDC中,BD=2
∴点D到AB所在直线的距离为2
(2)过B1作BD的垂线角BD与E,连接A1E,B1E
∵A1B1⊥侧面BC1,
∴∠A1EB1为二面角A1-BD-B1的平面角
在直角三角形A1B1E中,A1B1=1,B1E=
∴tan∠A1EB1=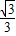
∴∠A1EB1=30°
即二面角A1-BD-B1的度数为30°
点评:本题主要考查了点到平面的距离,以及二面角的度量等有关知识,同时考查了空间想象能力、推理论证的能力,和转化与划归的思想,属于中档题.
(2)过B1作BD的垂线角BD与E,连接A1E,B1E,根据二面角平面角的定义可知∠A1EB1为二面角A1-BD-B1的平面角,在直角三角形A1B1E中,求出此角即可.
解答:
 解:(1)∵BD在底面的射影为BC
解:(1)∵BD在底面的射影为BC∴∠DBC即为BD与底面所成角则∠DBC=30°
∵∠B=90°,直三棱柱ABC-A1B1C1,
∴AB⊥侧面BC1,而BD?侧面BC1,
∴AB⊥BD即BD为点D到AB所在直线的距离
在直角三角形BDC中,BD=2
∴点D到AB所在直线的距离为2
(2)过B1作BD的垂线角BD与E,连接A1E,B1E
∵A1B1⊥侧面BC1,
∴∠A1EB1为二面角A1-BD-B1的平面角
在直角三角形A1B1E中,A1B1=1,B1E=

∴tan∠A1EB1=
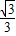
∴∠A1EB1=30°
即二面角A1-BD-B1的度数为30°
点评:本题主要考查了点到平面的距离,以及二面角的度量等有关知识,同时考查了空间想象能力、推理论证的能力,和转化与划归的思想,属于中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点. 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4. 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点. 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (2010•莒县模拟)如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CCl、AB中点.
(2010•莒县模拟)如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CCl、AB中点.