题目内容
如图,在每个三角形的顶点处各放置一个数,使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别成等差数列.若顶点A,B,C处的三个数互不相同且和为l,则所有顶点上的数之和等于 。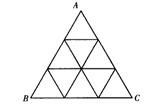

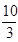
解:由题意可得,(各点放的数用该点的坐标表示)
当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1
2(D+E+F)=2(A+B+C)=2,D+E+F=1∴f(2)=2=(3×4)/ 6
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,,且A+B+C=1
从而可得D+E+H+I+F+F=2(A+B+C)=2
同样根据等差中项可得,M的数为1/ 3∴f(3)="3+1" /3 ="10/" 3 =4×5/ 6
同理可得,f(4)=5=5×6/ 6 f(n)="n(n+1)/" 6,
当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1
2(D+E+F)=2(A+B+C)=2,D+E+F=1∴f(2)=2=(3×4)/ 6
当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,,且A+B+C=1
从而可得D+E+H+I+F+F=2(A+B+C)=2
同样根据等差中项可得,M的数为1/ 3∴f(3)="3+1" /3 ="10/" 3 =4×5/ 6
同理可得,f(4)=5=5×6/ 6 f(n)="n(n+1)/" 6,

练习册系列答案
相关题目
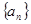 中,
中,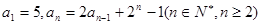 ,若存在实数
,若存在实数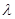 ,使得数列
,使得数列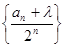 为等差数列,则
为等差数列,则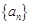 是各项均为正数的等差数列.
是各项均为正数的等差数列.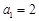 ,且
,且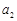 ,
,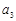 ,
,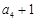 成等比数列,求数列
成等比数列,求数列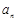 ;
;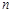 和为
和为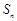 ,设
,设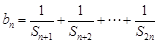 ,若对任意的
,若对任意的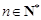 ,不等式
,不等式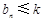 恒成立,求实数
恒成立,求实数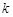 的最小值;
的最小值;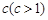 的不同次幂,求证:数列
的不同次幂,求证:数列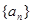 为等差数列,公差为
为等差数列,公差为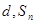 为其前
为其前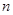 项和,
项和,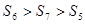 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )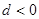
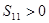
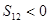
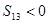
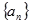 是公差不为零的等差数列,
是公差不为零的等差数列,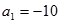 ,且
,且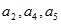 成等比数列.
成等比数列.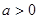 ,求数列
,求数列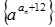 的前n项和
的前n项和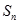 .
.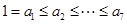 ,其中
,其中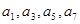 成公比为q的等比数列,
成公比为q的等比数列,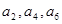 成公差为1的等差数列,则q的最小值是( )
成公差为1的等差数列,则q的最小值是( )



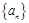 的公差不为零,
的公差不为零,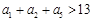 ,且
,且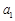 、
、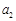 、
、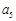 成等比数
成等比数 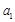 的取值范围为 .
的取值范围为 .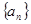 中,已知
中,已知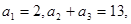 则
则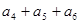 等于
等于