设a.b是两个实数,A={(x,y)|x=n,y=na+b,n∈Z},B={(x,y)|x=m,y=3m2+15,m∈Z},C={(x,y)|x2+y2≤144}都是平面xOy内的点的集合.求证:不存在a.b,使得A∩B≠,且点(a,b)∈C同时成立.? 题目和参考答案——青夏教育精英家教网—

题目内容

设a、b是两个实数,

A={(x,y)|x=n,y=na+b,n∈Z},

B={(x,y)|x=m,y=3m²+15,m∈Z},

C={(x,y)|x²+y²≤144}都是平面xOy内的点的集合.

求证:不存在a、b,使得A∩B≠,且点(a,b)∈C同时成立.?

解析:假设存在a、b,使A∩B≠,且点(a,b)∈C.?

由(a,b)∈C,得a²+b²≤144,①?

由A∩B≠得直线y=ax+b与抛物线y=3x²+15必有交点,且交点中至少有一点的横、纵坐标均为整数.因此由

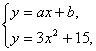得3x²-ax+15-b=0,?

Δ=a²-4×3(15-b)≥0.②?

由①②得144-b²≥a²≥4×3(15-b),于是144-b²≥12(15-b),(b-6)²≤0,b=6.?

从而a²=108,直线方程为y=x+6或y=-x+6,?直线上点的横、纵坐标不可能均为整数,这与假设相矛盾.所以假设不成立,原命题正确.

练习册系列答案

设a、b是两个实数，给出的下列条件中能推出“a、b中至少有一个数大于1”的条件是（　　）
①a+b＞1 ②a+b=2 ③a+b＞2 ④a²+b²＞2 ⑤ab＞1．

已知函数f1(x)=3|x-p1|，f2(x)=2•3|x-p2|（x∈R，p₁，p₂为常数）．函数f（x）定义为：对每个给定的实数x，f(x)=

f1(x)	若f1(x)≤f2(x)
f2(x)	若f1(x)＞f2(x)

（1）求f（x）=f₁（x）对所有实数x成立的充分必要条件（用p₁，p₂表示）；
（2）设a，b是两个实数，满足a＜b，且p₁，p₂∈（a，b）．若f（a）=f（b），求证：函数f（x）在区间[a，b]上的单调增区间的长度之和为

b-a

（闭区间[m，n]的长度定义为n-m）

已知函数f₁（x）=lg|x-p₁|，f₂（x）=lg（|x-p₂|+2）（x∈R，p₁，p₂为常数）
函数f（x）定义为对每个给定的实数x（x≠p₁），f(x)=

f1(x)	f1(x)≤f2(x)
f2(x)	f2(x)≤f1(x)

（1）当p₁=2时，求证：y=f₁（x）图象关于x=2对称；
（2）求f（x）=f₁（x）对所有实数x（x≠p₁）均成立的条件（用p₁、p₂表示）；
（3）设a，b是两个实数，满足a＜b，且p₁，p₂∈（a，b），若f（a）=f（b）求证：函数f（x）在区间[a，b]上单调增区间的长度之和为

b-a

．（区间[m，n]、（m，n）或（m，n]的长度均定义为n-m）

设a，b是两个实数，给出下列条件：
①a+b＞1；②a+b=2；③a+b＞2；④a²+b²＞2；⑤ab＞1．
其中能推出：“a，b中至少有一个大于1”的条件是（　　）

试题分类