题目内容
已知函数f1(x)=3|x-p1|,f2(x)=2•3|x-p2|(x∈R,p1,p2为常数).函数f(x)定义为:对每个给定的实数x,f(x)=
|
(1)求f(x)=f1(x)对所有实数x成立的充分必要条件(用p1,p2表示);
(2)设a,b是两个实数,满足a<b,且p1,p2∈(a,b).若f(a)=f(b),求证:函数f(x)在区间[a,b]上的单调增区间的长度之和为
| b-a |
| 2 |
分析:(1)根据题意,先证充分性:由f(x)的定义可知,f(x)=f1(x)对所有实数成立,等价于f1(x)≤f2(x)对所有实数x成立等价于3|x-p1|≤2•3|x-p2|,即3|x-p1|-|x-p2|≤3log32=2对所有实数x均成立,分析容易得证;再证必要性:3|x-p1|-|x-p2|≤3log32=2对所有实数x均成立等价于3|p1-p2|≤2,即|p1-p2|≤log32,
(2)分两种情形讨论:①当|p1-p2|≤log32时,由中值定理及函数的单调性得到函数f(x)在区间[a,b]上的单调增区间的长度;②当|p1-p2|>log32时,a,b是两个实数,满足a<b,且p1,p2∈(a,b).若f(a)=f(b),根据图象和函数的单调性得到函数f(x)在区间[a,b]上的单调增区间的长度.
(2)分两种情形讨论:①当|p1-p2|≤log32时,由中值定理及函数的单调性得到函数f(x)在区间[a,b]上的单调增区间的长度;②当|p1-p2|>log32时,a,b是两个实数,满足a<b,且p1,p2∈(a,b).若f(a)=f(b),根据图象和函数的单调性得到函数f(x)在区间[a,b]上的单调增区间的长度.
解答:解:(1)由f(x)的定义可知,f(x)=f1(x)(对所有实数x)等价于f1(x)≤f2(x)(对所有实数x)这又等价于3|x-p1|≤2•3|x-p2|,即3|x-p1|-|x-p2|≤3log32=2对所有实数x均成立.(*)
由于|x-p1|-|x-p2|≤|(x-p1)-(x-p2)|=|p1-p2|(x∈R)的最大值为|p1-p2|,
故(*)等价于3|p1-p2|≤2,即|p1-p2|≤log32,这就是所求的充分必要条件
(2)分两种情形讨论
(i)当|p1-p2|≤log32时,由(1)知f(x)=f1(x)(对所有实数x∈[a,b])
则由f(a)=f(b)及a<p1<b易知p1=
,
再由f1(x)=
的单调性可知,
函数f(x)在区间[a,b]上的单调增区间的长度
为b-
=
(参见示意图)
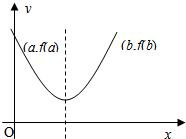
(ii)|p1-p2|>log32时,不妨设p1<p2,则p2-p1>log32,于是
当x≤p1时,有f1(x)=3p1-x<3p2-x<f2(x),从而f(x)=f1(x);
当x≥p2时,有f1(x)=3x-p1=3p2-p1+x-p2=3p2-p1•3x-p2>3log32•3x-p2=f2(x)
从而f(x)=f2(x);当p1<x<p2时,f1(x)=3x-p1,及f2(x)=2•3p2-x,由方程3x-p1=2•3p2-x
解得f1(x)与f2(x)图象交点的横坐标为x0=
+
log32(1)
显然p1<x0=p2-
[(p2-p1)-log32]<p2,
这表明x0在p1与p2之间.由(1)易知f(x)=
综上可知,在区间[a,b]上,f(x)=
(参见示意图)
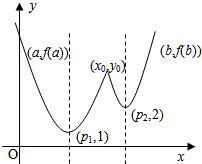
故由函数f1(x)及f2(x)的单调性可知,f(x)在区间[a,b]上的单调增区间的长度之和为(x0-p1)+(b-p2),由于f(a)=f(b),即3p1-a=2•3b-p2,得p1+p2=a+b+log32(2)
故由(1)、(2)得(x0-p1)+(b-p2)=b-
[p1+p2-log32]=
综合(i)(ii)可知,f(x)在区间[a,b]上的单调增区间的长度和为
.
由于|x-p1|-|x-p2|≤|(x-p1)-(x-p2)|=|p1-p2|(x∈R)的最大值为|p1-p2|,
故(*)等价于3|p1-p2|≤2,即|p1-p2|≤log32,这就是所求的充分必要条件
(2)分两种情形讨论
(i)当|p1-p2|≤log32时,由(1)知f(x)=f1(x)(对所有实数x∈[a,b])
则由f(a)=f(b)及a<p1<b易知p1=
| a+b |
| 2 |
再由f1(x)=
|
函数f(x)在区间[a,b]上的单调增区间的长度
为b-
| a+b |
| 2 |
| b-a |
| 2 |

(ii)|p1-p2|>log32时,不妨设p1<p2,则p2-p1>log32,于是
当x≤p1时,有f1(x)=3p1-x<3p2-x<f2(x),从而f(x)=f1(x);
当x≥p2时,有f1(x)=3x-p1=3p2-p1+x-p2=3p2-p1•3x-p2>3log32•3x-p2=f2(x)
从而f(x)=f2(x);当p1<x<p2时,f1(x)=3x-p1,及f2(x)=2•3p2-x,由方程3x-p1=2•3p2-x
解得f1(x)与f2(x)图象交点的横坐标为x0=
| p1+p2 |
| 2 |
| 1 |
| 2 |
显然p1<x0=p2-
| 1 |
| 2 |
这表明x0在p1与p2之间.由(1)易知f(x)=
|
综上可知,在区间[a,b]上,f(x)=
|

故由函数f1(x)及f2(x)的单调性可知,f(x)在区间[a,b]上的单调增区间的长度之和为(x0-p1)+(b-p2),由于f(a)=f(b),即3p1-a=2•3b-p2,得p1+p2=a+b+log32(2)
故由(1)、(2)得(x0-p1)+(b-p2)=b-
| 1 |
| 2 |
| b-a |
| 2 |
综合(i)(ii)可知,f(x)在区间[a,b]上的单调增区间的长度和为
| b-a |
| 2 |
点评:考查学生理解充分必要条件的证明方法,用数形结合的数学思想解决问题的能力,以及充分必要条件的证明方法.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目