题目内容
5.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A且斜率为k的直线交椭圆与另一个点B,且点B在x轴上的设影恰好为右焦点F,若0<k<$\frac{1}{3}$,则椭圆的离心率的取值范围是($\frac{2}{3}$,1).分析 先作出图形,则易知|AF2|=a+c,|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,再由∠BAF2是直线的倾斜角,易得k=tan∠BAF2=$\frac{a-c}{a}$,由k的范围,结合离心率公式化简求解.
解答 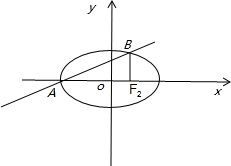 解:如图所示:|AF2|=a+c,
解:如图所示:|AF2|=a+c,
令x=c,可得y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=±$\frac{{a}^{2}-{c}^{2}}{a}$,
即有|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,
∴k=tan∠BAF2=$\frac{|B{F}_{2}|}{|A{F}_{2}|}$=$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$=$\frac{a-c}{a}$,
又∵0<k<$\frac{1}{3}$,
∴0<$\frac{a-c}{a}$<$\frac{1}{3}$,
∴0<1-e<$\frac{1}{3}$,
∴$\frac{2}{3}$<e<1,
故答案为:($\frac{2}{3}$,1).
点评 本题考查了椭圆与直线的位置关系及椭圆的几何性质和直线的斜率与倾斜角,属于中档题.

练习册系列答案
相关题目
15.已知曲线y=$\frac{1}{3}$x3+$\frac{4}{3}$,则在点P(2,4)的切线方程是( )
| A. | 4x-y-4=0 | B. | x-4y-4=0 | C. | 4x-4y-1=0 | D. | 4x+y-4=0 |
16.直线y=a分别与曲线y=2(x-1),y=x+ex交于A,B,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{5}}{5}$ |
20.下列函数中,是偶函数且在区间(0,+∞)上单调递减的是( )
| A. | y=-3|x| | B. | y=x${\;}^{\frac{1}{3}}$ | C. | y=log3x2 | D. | y=x-x2 |
6.函数$y=2sin(2x+\frac{π}{2})$是( )
| A. | 周期为$\frac{π}{2}$的奇函数 | B. | 周期为$\frac{π}{2}$的偶函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为π的奇函数 |