题目内容
15.在区间(0,1)中,随机的取出两个数,其和小于$\frac{1}{2}$的概率为( )| A. | $\frac{7}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
分析 设取出的两个数为x、y,则可得“0<x<1,0<y<1”表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,而x+y<$\frac{1}{2}$表示的区域为直线x+y=$\frac{1}{2}$下方,分别计算其面积,由几何概型的计算公式可得答案
解答  解:设取出的两个数为x、y,则有0<x<1,0<y<1,其表示的区域为纵横坐标都在(0,1)之间的正方形区域,
解:设取出的两个数为x、y,则有0<x<1,0<y<1,其表示的区域为纵横坐标都在(0,1)之间的正方形区域,
得其面积为1,
而x+y<$\frac{1}{2}$表示的区域为直线x+y=$\frac{1}{2}$下方,且在0<x<1,0<y<1表示区域内部的部分,
其中E(0,$\frac{1}{2}$),D($\frac{1}{2}$,0)
则对应△OED的面积S=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{8}$,
则两数之和小于$\frac{1}{2}$的概率是$\frac{\frac{1}{8}}{1×1}$=$\frac{1}{8}$,
故选:B
点评 本题考查几何概型的计算,解题的关键在于用平面区域表示出题干的代数关系,求出对应的面积是解决本题的关键..

练习册系列答案
相关题目
5.下列函数是奇函数的是( )
| A. | y=x2+1 | B. | y=sinx | C. | y=log2(x+5) | D. | y=2x-3 |
6.当-π≤x≤0时,函数$f(x)=sinx+\sqrt{3}cosx$最小值为( )
| A. | -1 | B. | -2 | C. | $-\sqrt{3}$ | D. | 0 |
20.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到我市周一至周五某一时间段车流量与PM2.5的数据如表
(Ⅰ)根据表中数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(Ⅱ)规定当一天内PM2.5的浓度平均值在(0,35]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(35,75]内,空气质量等级为良.为使我国某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内?(结果保留整数)
附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 59 | 55 | 52 | 51 | 58 |
| PM2.5的浓度平均值y(微克/立方米) | 81 | 67 | 66 | 59 | 77 |
(Ⅱ)规定当一天内PM2.5的浓度平均值在(0,35]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(35,75]内,空气质量等级为良.为使我国某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内?(结果保留整数)
附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
4.设t是函数f(x)=ex+lnx的零点,若x0>t,则f(x0)的值满足( )
| A. | f(x0)=0 | B. | f(x0)>0 | C. | f(x0)<0 | D. | f(x0)的符号不确定 |
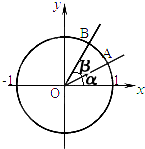 如图,在平面直角坐标系中,锐角a、β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角a、β的终边分别与单位圆交于A、B两点.