题目内容
10.在△ABC中,角A,B,C的对边长为a,b,c,已知b+c=1+$\sqrt{2}$,∠B=30°,∠C=45°,则a=$\frac{{\sqrt{6}+\sqrt{2}}}{2}$.分析 作CD⊥AB于点D.设CD=x,利用三角函数表示出a、b,然后根据b+c=1+$\sqrt{2}$,列方程求得x的值,进而求得c的值.
解答 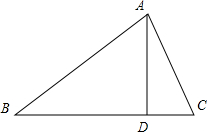 解:作AD⊥BC于点D.
解:作AD⊥BC于点D.
设AD=x,
在直角△ABD中,∠B=30°,则AB=2AD=2x,BD=$\sqrt{3}$x,
在直角△ACD中,∠C=45°,则AC=$\sqrt{2}$AD=$\sqrt{2}$x,CD=AD=x,
∵b+c=1+$\sqrt{2}$,
∴2x+$\sqrt{2}$x=1+$\sqrt{2}$,
解得:x=$\frac{\sqrt{2}}{2}$,
故a=BD+DC=$\sqrt{3}×\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$=$\frac{{\sqrt{6}+\sqrt{2}}}{2}$.
故答案为:$\frac{{\sqrt{6}+\sqrt{2}}}{2}$.
点评 本题考查了解直角三角形中三角函数的应用,熟练掌握好边角之间的关系是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
1.tan75°=( )
| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
18.设2a=3,2b=6,2c=12,则数列a,b,c是( )
| A. | 是等差数列,但不是等比数列 | B. | 是等比数列,但不是等差数列 | ||
| C. | 既是等差数列,又是等比数列 | D. | 非等差数列,又非等比数列 |
15.在区间(0,1)中,随机的取出两个数,其和小于$\frac{1}{2}$的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
2.已知函数f(x)在R上可导,下列四个选项中正确的是( )
| A. | 若f(x)>f′(x)对x∈R恒成立,则 ef(1)<f(2) | |
| B. | 若f(x)<f′(x)对x∈R恒成立,则e2f(-1)>f(1) | |
| C. | 若f(x)+f′(x)>0对x∈R恒成立,则ef(2)<f(1) | |
| D. | 若f(x)+f′(x)<0对x∈R恒成立,则f(-1)>e2f(1) |
 如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).
如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).