题目内容
17.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是( )| A. | 0.26 | B. | 0.08 | C. | 0.18 | D. | 0.72 |
分析 由条件利用相互独立事件的概率乘法公式求得甲种子发芽而乙种子不发芽的概率、乙种子发芽而甲种子不发芽的概率,再把这两个概率值相加,即得所求.
解答 解:甲种子发芽而乙种子不发芽的概率为0.8×0.1=0.08,
乙种子发芽而甲种子不发芽的概率为0.9×0.2=0.18,
故恰有一粒种子能发芽的概率是0.08+0.18=0.26,
故选:A.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件与它的对立事件概率间的关系,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
7.某地近几年粮食需求量逐年上升,如表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)({y}_{1}-y)}{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}{y}_{1})-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$,$\widehat{a}$=$\widehat{y}-\widehat{b}x$)
| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 286 | 298 | 318 |
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)({y}_{1}-y)}{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}{y}_{1})-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$,$\widehat{a}$=$\widehat{y}-\widehat{b}x$)
9.已知F1,F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,P为椭圆上一点,且PF2垂直于x轴.若|F1F2|=2|PF2|,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
6.4位同学要完成100米的接力跑,要求每个人跑的路程不超过其他任一同学所跑路程的3倍,若某一同学所跑路程为x米,则x的取值范围为( )
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.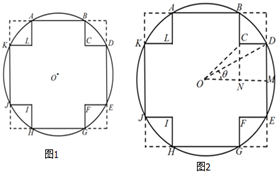 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)