题目内容
4.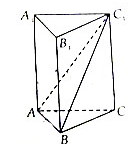 如图所示,在正三棱柱ABC-A1B1C1中,AB=1,CC1=$\sqrt{3}$.
如图所示,在正三棱柱ABC-A1B1C1中,AB=1,CC1=$\sqrt{3}$.(1)求证:A1B1∥平面ABC;
(2)求二面角C-AB-C1的大小的正切值.
分析 (1)根据棱柱的定义便知,两底面平行,从而便可得出A1B1∥平面ABC;
(2)可先找出二面角C-AB-C1的平面角:容易发现取AB的中点D,连接CD,C1D,这样根据该三棱柱为正三棱柱及二面角平面角的定义即可得出∠CDC1便是要找的二面角的平面角,而容易看出△CC1D为直角三角形,CD可以求出,CC1=$\sqrt{3}$,这样即可求出tan∠CDC1.
解答 解:(1)证明:正三棱柱的两底面互相平行,即平面A1B1C1∥平面ABC;
又A1B1?平面A1B1C1;
∴A1B1∥平面ABC;
(2)如图,取AB的中点D,连接CD,C1D;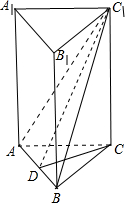
∵AC=BC,AC1=BC1;
∴CD⊥AB,C1D⊥AB;
∴∠C1DC为二面角C-AB-C1的平面角;
根据题意,△ABC为等边三角形,边长为1,∴$CD=1•sin60°=\frac{\sqrt{3}}{2}$;
CC1⊥底面ABC,CD?底面ABC;
∴CC1⊥CD;
又$C{C}_{1}=\sqrt{3}$;
∴在Rt△C1CD中,tan$∠{C}_{1}DC=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$;
即二面角C-AB-C1的大小的正切值为2.
点评 考查棱柱的定义,正三棱柱的定义,以及二面角及二面角的平面角的定义及求法,线面垂直的性质,正切函数的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.若|$\overrightarrow{e}$|=1,且$\overrightarrow{a}⊥\overrightarrow{e}$,|$\overrightarrow{a}$|=2,则|4$\overrightarrow{a}-\overrightarrow{e}$|=( )
| A. | $\sqrt{37}$ | B. | $\sqrt{65}$ | C. | 8 | D. | $\sqrt{13}$ |