题目内容
2.分别以一个直角三角形的斜边,两直角边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,画出它们的三视图和直观图,并探讨它们体积之间的关系.分析 如图所示三视图和直观图,其体积分别为:Va=$\frac{1}{3}π{a}^{2}b$,Vb=$\frac{1}{3}π{b}^{2}a$,Vc=$\frac{1}{3}π•\frac{{a}^{2}{b}^{2}}{c}$.不妨设c>a≥b,可得a2b≥ab2>$\frac{{a}^{2}{b}^{2}}{c}$,即可得出大小关系.
解答 解:如图所示,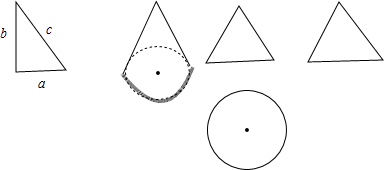
(1)分别以直角边a,b所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,它们的三视图和直观图,其体积分别为:Va=$\frac{1}{3}π{a}^{2}b$,Vb=$\frac{1}{3}π{b}^{2}a$.
(2)以一个直角三角形的斜边c所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,它们的三视图和直观图,Vc=$\frac{1}{3}π(\frac{ab}{c})^{2}•c$=$\frac{1}{3}π•\frac{{a}^{2}{b}^{2}}{c}$.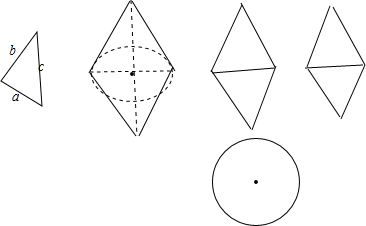
(3)不妨设c>a≥b,
则a2b≥ab2>$\frac{{a}^{2}{b}^{2}}{c}$,
∴Va≥Vb>Vc.
点评 本题考查了圆锥的三视图及其直观图、圆锥体积计算公式、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
10.已知全集U=R集合A={x|log2(x-1)},B={y|y=2x},则(CUA)∩B=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1) | D. | (1,2) |
7.已知b,c∈R,函数f(x)=x2+bx+c,方程f(x)-x=0的两个实根为x1,x2,且x2-x1>2,若四次方程f(f(x))=x的另两个根为x3,x4(其中x3<x4),则( )
| A. | x1<x2<x3<x4 | B. | x3<x1<x4<x2 | C. | x1<x3<x4<x2 | D. | x1<x3<x2<x4 |