题目内容

4．已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的两个焦点为F1，F2，P为椭圆上一点，且PF1⊥PF2，则|PF1|•|PF2|的值为（　　）
A．48B．24C．36D．25

分析 利用椭圆的定义及勾股定理，即可得出结论．

解答 解：设|PF1|=m，|PF2|=n，则m+n=14，m2+n2=100，
∴2mn=（m+n）2-（m2+n2）=96，
∴mn=48，即|PF1|•|PF2|=48．
故选：A．

点评 本题考查椭圆的定义，考查勾股定理，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
13．已知等比数列{an}的各项都为正数，若a1+a2+a3+a4+a5+a6=1，$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{4}}$+$\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{6}}$=10，则a1•a2•a3•a4•a5•a6=$\frac{1}{1000}$．
14．已知函数f（x）=x3+x，对任意的m∈[-2，2]，f（mx-2）+f（x）＜0恒成立，则x的取值范围为（-2，$\frac{2}{3}$）．
12．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）及内部面积为S=πab，A1，A2是长轴的两个顶点，B1，B2是短轴的两个顶点，在椭圆上或椭圆内部随机取一点 P，给出下列命题：
①△PA1A2为钝角三角形的概率为1；
②△PB1B2为钝角三角形的概率为$\frac{b}{a}$；
③△PA1A2为钝角三角形的概率为$\frac{b}{a}$； 
④△PB1B2为锐角三角形的概率为$\frac{a-b}{a}$．
其中正确的命题有①②④．（填上你认为所有正确的命题序号）
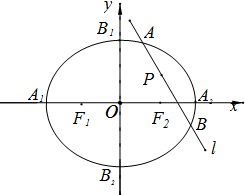19．如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的顶点为A1，A2，B1B2，焦点为F1，F2，a2+b2=7
S${\;}_{?{A}_{1}{B}_{1}{A}_{2}{B}_{2}}$=2S${\;}_{?{B}_{1}{F}_{1}{B}_{2}{F}_{2}}$
（1）求椭圆C的方程；
（2）设直线m过P（1，1），且与椭圆相交于A，B两点，当P是A，B的中点时，求直线m的方程．
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，一个焦点与抛物线y2=4x的焦点重合，直线l：y=kx+m与椭圆C相交于A、B两点．
（1）求椭圆C的标准方程；
（2）设O为坐标原点，kOA•kOB=-$\frac{{b}^{2}}{{a}^{2}}$，判断△AOB的面积是否为定值？若是，求出定值，若不是，说明理由．
16．若椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，点（1，$\frac{3}{2}$）在椭圆C上．
（1）求椭圆C的方程；
（2）过椭圆右焦点F2 斜率为k（k≠0的直线l与椭圆C相交于E，F两点，A为椭圆的右顶点，直线AE，AF分别交直线x=3于点M，N，线段MN的中点为P，记直线PF2 的斜率为k′，求证：k•k′为定值．
13．已知函数f（x）的对应关系如表所示，则f[f（5）]的值为（　　）
x12345
f（x）54312
A．1B．2C．4D．5
14．设命题p：函数3x2-a≤0在区间[-1，1]上恒成立，命题q：函数y=x2-ax+1的最小值不大于0．如果命题p或q为真命题，p且q为假命题，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网