题目内容
15.空间四点A,B,C,D满足|$\overrightarrow{AB}$|=2,|$\overrightarrow{BC}$|=3,|$\overrightarrow{CD}$|=4,|$\overrightarrow{DA}$|=7,则$\overrightarrow{AC}$•$\overrightarrow{BD}$的值为19.分析 将向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{CD}$,$\overrightarrow{DA}$转化为以$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OD}$的式子,计算|$\overrightarrow{AB}$|2-|$\overrightarrow{BC}$|2+|$\overrightarrow{CD}$|2-|$\overrightarrow{DA}$|2,又$\overrightarrow{AC}$•$\overrightarrow{BD}$=($\overrightarrow{OC}$-$\overrightarrow{OA}$)•($\overrightarrow{OD}$-$\overrightarrow{OB}$),展开即可得到所求值.
解答 解:|$\overrightarrow{AB}$|2-|$\overrightarrow{BC}$|2+|$\overrightarrow{CD}$|2-|$\overrightarrow{DA}$|2=($\overrightarrow{AB}$)2-($\overrightarrow{BC}$)2+($\overrightarrow{CD}$)2-($\overrightarrow{DA}$)2
=($\overrightarrow{OB}$-$\overrightarrow{OA}$)2-($\overrightarrow{OB}$-$\overrightarrow{OC}$)2+($\overrightarrow{OD}$-$\overrightarrow{OC}$)2-($\overrightarrow{OA}$-$\overrightarrow{OD}$)2
=2($\overrightarrow{OC}$•$\overrightarrow{OB}$+$\overrightarrow{OA}$•$\overrightarrow{OD}$-$\overrightarrow{OA}$•$\overrightarrow{OB}$-$\overrightarrow{OC}$•$\overrightarrow{OD}$)
=4-9+16-49=-38,
即有$\overrightarrow{OC}$•$\overrightarrow{OB}$+$\overrightarrow{OA}$•$\overrightarrow{OD}$-$\overrightarrow{OA}$•$\overrightarrow{OB}$-$\overrightarrow{OC}$•$\overrightarrow{OD}$=-19,
又$\overrightarrow{AC}$•$\overrightarrow{BD}$=($\overrightarrow{OC}$-$\overrightarrow{OA}$)•($\overrightarrow{OD}$-$\overrightarrow{OB}$)
=$\overrightarrow{OC}$•$\overrightarrow{OD}$+$\overrightarrow{OA}$•$\overrightarrow{OB}$-$\overrightarrow{OC}$•$\overrightarrow{OB}$-$\overrightarrow{OA}$•$\overrightarrow{OD}$=19.
故答案为:19.
点评 本题考查向量的加减运算和数量积的性质,考查运算能力,属于中档题.

| A. | ∅ | B. | {y|y≥0} | C. | {(2,4),(-1,1)} | D. | {y|y>0} |
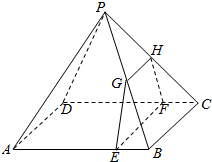 如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.