题目内容
14．已知f（x）=ax，g（x）=loga|x|（a＞0，且a≠1），若f（2014）•g（-2014）＜0，则y=f（x）与y=g（x）在同一坐标系内的大致图形是（ ）| A． |  | B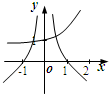． |  | C． |  | D． |  |
分析 由f（2014）•g（-2014）＜0可得g（-2014）＜0，即loga2014＜0，得出0＜a＜1．根据函数单调性可得出答案．
解答 解：∵f（2014）•g（-2014）＜0，f（2014）=a2014＞0，
∴g（-2014）=g（2014）＜0，即loga2014＜0，
∴0＜a＜1．
∴f（x）是减函数，g（x）在（0，+∞）上是减函数，
故选：A．
点评 本题考查了指数函数，对数函数的性质，找到a的范围是关键．
练习册系列答案
相关题目
已知函数f（x）=$\left\{\begin{array}{l}{|4-{x}^{2}|，x≤0}\\{{2}^{2-x}，0＜x≤2}\\{lo{g}_{2}x，x＞2}\end{array}\right.$，
5．已知集合M={y|y=x+2}，N={（x，y）|y=x2}，则M∩N=（ ）
| A． | ∅ | B． | {y|y≥0} | C． | {（2，4），（-1，1）} | D． | {y|y＞0} |
9．直角坐标系中，点$（1，-\sqrt{3}）$的极坐标可以是（ ）
| A． | $（2，\frac{4π}{3}）$ | B． | $（2，\frac{5π}{3}）$ | C． | $（2，\frac{5π}{6}）$ | D． | $（2，\frac{11π}{6}）$ |
19．下列命题中不正确的是（ ）
| A． | logab•logbc•logca=1（a，b，c均为不等于1的正数） | |
| B． | 若xlog34=1，则${4^x}+{4^{-x}}=\frac{10}{3}$ | |
| C． | 函数f（x）=lnx满足f（a+b）=f（a）•f（b）（a，b＞0） | |
| D． | 函数f（x）=lnx满足f（a•b）=f（a）+f（b）（a，b＞0） |