题目内容
已知n为正偶数,用数学归纳法证明( )
1 时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
1
 时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )| A.n=k+1时等式成立 | B.n=k+2时等式成立 |
| C.n=2k+2时等式成立 | D.n=2(k+2)时等式成立 |
B
分析:首先分析题目因为n为正偶数,用数学归纳法证明的时候,若已假设n=k(k≥2,k为偶数)时命题为真时,因为n取偶数,则n=k+1代入无意义,故还需要证明n=k+2成立.
解:若已假设n=k(k≥2,k为偶数)时命题为真,因为n只能取偶数,所以还需要证明n=k+2成立.
故选B.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,数列
,数列 满足:
满足: 。
。 ;
; ;
;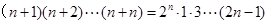 (
(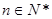 )时,从“
)时,从“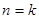 到
到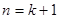 ”左边需增乘的代数式为( )
”左边需增乘的代数式为( )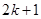
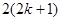
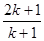
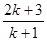
 .
. 与Sn+1的大小,并说明理由.
与Sn+1的大小,并说明理由.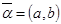 ,
,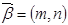 ,其中
,其中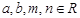 ,由不等式
,由不等式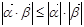 恒成立,可以证明(柯西)不等式
恒成立,可以证明(柯西)不等式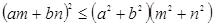 (当且仅当
(当且仅当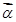 ∥
∥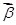 ,即
,即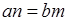 时等号成立),己知
时等号成立),己知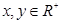 ,若
,若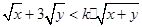 恒成立,利用可西不等式可求得实数
恒成立,利用可西不等式可求得实数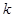 的取值范围是
的取值范围是  成立,起始值至少应取为( )
成立,起始值至少应取为( )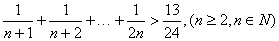 ”的过程中,
”的过程中,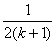
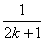 和
和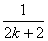

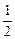 ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.
,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.