题目内容
11.已知函数f(x)=$\frac{2{x}^{2}-kx+k}{{e}^{x}}$.(1)当k为何值时,f(x)在R上是减函数;
(2)试确定实数k的值,使f(x)的极小值为0.
分析 (1)求出导数,由题意可得-2x2+(4+k)x-2k≤0恒成立,运用判别式小于等于0,解不等式即可得到所求值;
(2)求出导数,对k讨论,当k>4时,当k<4时,求得单调区间,即可得到极小值,解方程即可得到所求k的值.
解答 解:(1)函数f(x)=$\frac{2{x}^{2}-kx+k}{{e}^{x}}$的导数为
f′(x)=$\frac{-2{x}^{2}+(4+k)x-2k}{{e}^{x}}$,
由f′(x)≤0在R上恒成立,可得-2x2+(4+k)x-2k≤0恒成立,
即有判别式△=(4+k)2-16k≤0,
解得(k-4)2≤0,由(k-4)2≥0,
解得k=4.
即有当k为4时,f(x)在R上是减函数;
(2)由于f′(x)=$\frac{-2{x}^{2}+(4+k)x-2k}{{e}^{x}}$,
由-2x2+(4+k)x-2k=-2(x-2)(x-$\frac{k}{2}$),(k≠4),
当k>4时,由f′(x)>0可得2<x<$\frac{k}{2}$;由f′(x)<0可得x>$\frac{k}{2}$或x<2.
可得x=2处取得极小值,且有f(2)=0,
即8-2k+k=0,解得k=8,成立;
当k<4时,由f′(x)>0可得$\frac{k}{2}$<x<2;由f′(x)<0可得x<$\frac{k}{2}$或x>2.
可得x=$\frac{k}{2}$处取得极小值,且有f($\frac{k}{2}$)=0,
即$\frac{{k}^{2}}{2}$-$\frac{{k}^{2}}{2}$+k=0,解得k=0,成立.
综上可得,当实数k的值为0和8,使f(x)的极小值为0.
点评 本题考查导数的运用:求单调区间和极值,同时考查函数的单调性的运用和不等式恒成立问题的解法,考查运算能力,属于中档题.

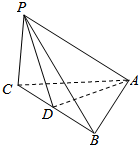 如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.
如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.