题目内容
【题目】设f（x）=aex+ 
+b（a＞0）．
（1）求f（x）在[0，+∞）上的最小值；
（2）设曲线y=f（x）在点（2，f（2））的切线方程为3x﹣2y=0，求a、b的值．
【答案】
（1）解：设t=ex（t≥1），
则y=at+ 
+by′=a﹣ 
= 
，
①a≥1时，y′＞0y=at+ +b在t≥1上递增，
得：t=1即x=0时，f（x）的最小值是a+ 
+b；
②0＜a＜1时，y=at+ +b≥2+b，
当且仅当at=1（t=ex= ，x=﹣lna）时，f（x）的最小值是b+2
（2）解：f（x）=aex+ 
+bf′（x）=aex﹣ ，
由题意得：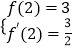 
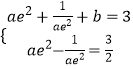
【解析】（1）设t=ex（t≥1），求出函数的导数，通过讨论a的范围，求出函数的最小值即可；（2）求出函数的导数，得到关于a，b的方程组，解出即可．
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
练习册系列答案
相关题目
【题目】某投资公司现提供两种一年期投资理财方案，一年后投资盈亏的情况如下表：
投资股市 | 获利 | 不赔不赚 | 亏损 | 购买基金 | 获利 | 不赔不赚 | 亏损 | |
概率 |
|
|
| 概率 |
|
|
|
（Ⅰ）甲、乙两人在投资顾问的建议下分别选择“投资股市”和“买基金”，若一年后他们中至少有一人盈利的概率大于
，求
的取值范围；
（Ⅱ）若
，某人现有
万元资金，决定在“投资股市”和“购买基金”这两种方案中选择出一种，那么选择何种方案可使得一年后的投资收益的数学期望值较大.
