题目内容
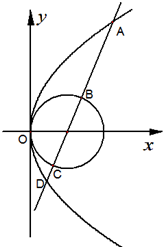 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l交C1于A,D两点,交C2于B,C两点,如图.
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l交C1于A,D两点,交C2于B,C两点,如图.(1)求|AB|•|CD|的值;
(2)是否存在直线l,使kOA+kOB+kOC+kOD=3
| 2 |
分析:(1)设直线l:my=x-1,A(x1,y1),D(x2,y2),由
⇒y2-4my-4=0,能求出|AB|•|CD|的值.
(2)设A(x1,y1),D(x2,y2),B(x3,y3),D(x4,y4),由kOA+kOD=
+
=
=
=-4m,知
⇒y2=
,由此能求出存在直线它的方程为
x+y-
=0.
|
(2)设A(x1,y1),D(x2,y2),B(x3,y3),D(x4,y4),由kOA+kOD=
| y1 |
| x1 |
| y2 |
| x2 |
| x1y2+x2y1 |
| x1x2 |
| y1y2(y1+y2) |
| 4x1x2 |
|
| 1 |
| 1+m2 |
| 2 |
| 2 |
解答:解:(1)设直线l:my=x-1,A(x1,y1),D(x2,y2)
由
⇒y2-4my-4=0,
得到y1y2=-4,x1x2=1,
∴|AB|•|CD|=(x1+1-1)(x2+1-1)=x1x2=1.…(6分)
(2)设A(x1,y1),D(x2,y2),B(x3,y3),D(x4,y4)
由(1)知
⇒y2=
,B(1+
,
),
∴C(1-
,-
),
∴kOB+kOC=
+
=
=-2m,
∴m=-
,
此时直线l:-
y=x-1,
由
⇒y2+2
y-4=0,
∴|AD|=
|y1-y2|=6,
|AB|+|CD|=2|BC|?|AD|=3|BC|=6,
所以|AB|,|BC|,|CD|成等差数列,
所以存在直线它的方程为
x+y-
=0.…(15分)
由
|
得到y1y2=-4,x1x2=1,
∴|AB|•|CD|=(x1+1-1)(x2+1-1)=x1x2=1.…(6分)
(2)设A(x1,y1),D(x2,y2),B(x3,y3),D(x4,y4)
由(1)知
|
| 1 |
| 1+m2 |
| m | ||
|
| 1 | ||
|
∴C(1-
| m | ||
|
| 1 | ||
|
∴kOB+kOC=
| y3 |
| x3 |
| y4 |
| x4 |
| x1y2+x2y1 |
| x1x2 |
∴m=-
| ||
| 2 |
此时直线l:-
| ||
| 2 |
由
|
| 2 |
∴|AD|=
| 1+m2 |
|AB|+|CD|=2|BC|?|AD|=3|BC|=6,
所以|AB|,|BC|,|CD|成等差数列,
所以存在直线它的方程为
| 2 |
| 2 |
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (2012•河北模拟)已知抛物线C1:y2=2px和圆
(2012•河北模拟)已知抛物线C1:y2=2px和圆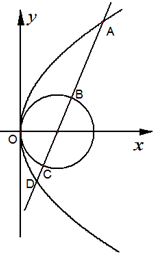 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).