题目内容
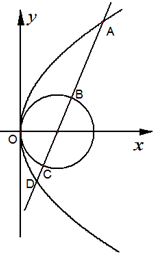 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).(Ⅰ)求|AB|•|CD|的值;
(Ⅱ)设直线OA、OB、OC、OD的斜率分别为m、n、p、q,且满足m+n+p+q=3
| 2 |
分析:(1)利用抛物线的定义和|AF|=|AB|+1就可得出|AB|=xA,同理可得:|CD|=xD,要分l⊥x轴和l不垂直x轴两种情况分别求值,当l⊥x轴时易求,当l不垂直x轴时,将直线的方程代入抛物线方程,利用根与系数关系可求得.
(2)首先在第1问得基础上和|AB|,|BC|,|CD|成等差数的关系用坐标表示,就可得出k的值,然后再把m+n+p+q=3
用坐标表示,再联立直线和圆的方程利用根与系数关系,把几个坐标的关系式联合起来就可确定k的值,从而求出此时的直线方程.
(2)首先在第1问得基础上和|AB|,|BC|,|CD|成等差数的关系用坐标表示,就可得出k的值,然后再把m+n+p+q=3
| 2 |
解答:解:(1)∵y2=4x,焦点F(1,0),准线 l0:x=-1.
由定义得:|AF|=xA+1,又∵|AF|=|AB|+1,∴|AB|=xA同理:|CD|=xD
当l⊥x轴时,则xD=xA=1,∴|AB|×|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,∴xAxD=1,∴|AB|×|CD|=1
综上所述,|AB|×|CD|=1
(2)∵|AB|,|BC|,|CD|成等差,且|AB|=xA,|BC|=2,|CD|=xD,∴xA+xD=4
由(1)得:xA+xD=
, ∴k2=2,∴k=±
∵l:y=k(x-1),∴m=kOA=
=k(1-
)
同理:n=k(1-
) ,p=k(1-
) ,q=k(1-
)
∴m+n+p+q=k[4-(
+
)-(
+
)]=3
又
+
=
=4
把y=k(x-1)代入(x-1)2+y2=1得,(k2+1)x2-2(1+k2)x+k2=1,∵k2=2,∴3x2-6x+2=0
∴xB+xC=2, xBxC=
,
+
=3, ∴K=-
,
所以所求直线L的方程为
x+y-
=0
由定义得:|AF|=xA+1,又∵|AF|=|AB|+1,∴|AB|=xA同理:|CD|=xD
当l⊥x轴时,则xD=xA=1,∴|AB|×|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,∴xAxD=1,∴|AB|×|CD|=1
综上所述,|AB|×|CD|=1
(2)∵|AB|,|BC|,|CD|成等差,且|AB|=xA,|BC|=2,|CD|=xD,∴xA+xD=4
由(1)得:xA+xD=
| 2k2+4 |
| k2 |
| 2 |
∵l:y=k(x-1),∴m=kOA=
| yA |
| xA |
| 1 |
| xA |
同理:n=k(1-
| 1 |
| xB |
| 1 |
| xC |
| 1 |
| xD |
∴m+n+p+q=k[4-(
| 1 |
| xA |
| 1 |
| xD |
| 1 |
| xB |
| 1 |
| xC |
| 2 |
又
| 1 |
| xA |
| 1 |
| xD |
| xA+xD |
| xAxD |
把y=k(x-1)代入(x-1)2+y2=1得,(k2+1)x2-2(1+k2)x+k2=1,∵k2=2,∴3x2-6x+2=0
∴xB+xC=2, xBxC=
| 2 |
| 3 |
| 1 |
| xB |
| 1 |
| xC |
| 2 |
所以所求直线L的方程为
| 2 |
| 2 |
点评:本题主要考查抛物线的定义、一元二次方程的根与系数关系,好在本题还融和了等差数列,主题思路是转化成坐标关系式,用方程的思想去解决.

练习册系列答案
相关题目
 (2012•河北模拟)已知抛物线C1:y2=2px和圆
(2012•河北模拟)已知抛物线C1:y2=2px和圆