题目内容
已知抛物线C1：y2=2px（p＞0）的焦点F以及椭圆C2：
+
=1，(a＞b＞0)的上、下焦点及左、右顶点均在圆O：x2+y2=1上．
（Ⅰ）求抛物线C1和椭圆C2的标准方程；
（Ⅱ）过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
=λ1
，
=λ2
，求证：λ1+λ2为定值．
（Ⅲ）直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P'、Q'，
•
+
•
+1=0，若点S满足：
=
+
，证明：点S在椭圆C2上．
| y2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）求抛物线C1和椭圆C2的标准方程；
（Ⅱ）过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
| NA |
| AF |
| NB |
| BF |
（Ⅲ）直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P'、Q'，
| OP |
| OQ |
| OP′ |
| OQ′ |
| OS |
| OP |
| OQ |
分析：（Ⅰ）由C1：y2=2px（p＞0）焦点F（
，0）在圆O：x2+y2=1上，可求p的值；同理由椭圆的上、下焦点（0，c），（0，-c）及左、右顶点（-b，0），（b，0）均在圆O：x2+y2=1上可解得椭圆C2的方程；
（Ⅱ）设直线AB的方程与抛物线联立，消元，利用韦达定理，结合
=λ1
，
=λ2
，从而可求λ1、λ2的值，即可得证；
（Ⅲ）设P，Q的坐标，利用
=
+
，确定S的坐标，利用
•
+
•
+1=0及P，Q在椭圆上，即可证得结论．
| p |
| 2 |
（Ⅱ）设直线AB的方程与抛物线联立，消元，利用韦达定理，结合
| NA |
| AF |
| NB |
| BF |
（Ⅲ）设P，Q的坐标，利用
| OS |
| OP |
| OQ |
| OP |
| OQ |
| OP′ |
| OQ′ |
解答：（Ⅰ）解：由C1：y2=2px（p＞0）焦点F（
，0）在圆O：x2+y2=1上得：
=1，∴p=2
∴抛物线C1：y2=4x…（2分）
同理由椭圆C2：
+
=1，(a＞b＞0)的上、下焦点（0，c），（0，-c）及左、右顶点（-b，0），（b，0）均在圆O：x2+y2=1上可解得：b=c=1，a=
∴椭圆C2：x2+
=1
（Ⅱ）证明：设直线AB的方程为y=k（x-1），A（x1，y1），B（x2，y2），则N（0，-k）
直线与抛物线联立，消元可得k2x2-（2k2+4）x+k2=0
∴x1+x2=
，x1x2=1
∵
=λ1
，
=λ2
∴λ1（1-x1）=x1，λ2（1-x2）=x2
∴λ1=
，λ2=
∴λ1+λ2=
=-1为定值；
（Ⅲ）证明：设P（x3，y3），Q（x4，y4），则P′（x3，0），Q′（x4，0），
∵
=
+
，∴S（x3+x4，y3+y4）
∵
•
+
•
+1=0
∴2x3x4+y3y4=-1①
∵P，Q在椭圆上，∴
+
=1②，
+
=1③
由①+②+③得（x3+x4）2+
=1
∴点S在椭圆C2上
| p |
| 2 |
| p2 |
| 4 |
∴抛物线C1：y2=4x…（2分）
同理由椭圆C2：
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
∴椭圆C2：x2+
| y2 |
| 2 |
（Ⅱ）证明：设直线AB的方程为y=k（x-1），A（x1，y1），B（x2，y2），则N（0，-k）
直线与抛物线联立，消元可得k2x2-（2k2+4）x+k2=0
∴x1+x2=
| 2k2+4 |
| k2 |
∵
| NA |
| AF |
| NB |
| BF |
∴λ1（1-x1）=x1，λ2（1-x2）=x2
∴λ1=
| x1 |
| 1-x1 |
| x2 |
| 1-x2 |
∴λ1+λ2=
| (x1+x2)-2x1x2 |
| 1-(x1+x2)+x1x2 |
（Ⅲ）证明：设P（x3，y3），Q（x4，y4），则P′（x3，0），Q′（x4，0），
∵
| OS |
| OP |
| OQ |
∵
| OP |
| OQ |
| OP′ |
| OQ′ |
∴2x3x4+y3y4=-1①
∵P，Q在椭圆上，∴
| x | 2 3 |
| ||
| 2 |
| x | 2 4 |
| ||
| 2 |
由①+②+③得（x3+x4）2+
| (y3+y4)2 |
| 2 |
∴点S在椭圆C2上
点评：本题考查抛物线与椭圆的方程，考查直线与椭圆的位置关系，考查向量知识的运用，解题的关键是联立方程，利用向量知识求解．
练习册系列答案
阅读快车系列答案
相关题目
（2012•河北模拟）已知抛物线C1：y2=2px和圆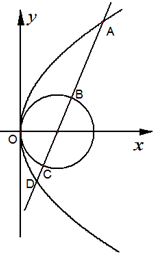
已知抛物线C1：y2=4x，圆C2：（x-1）2+y2=1，过抛物线焦点F的直线l交C1于A，D两点（点A在x轴上方），直线l交C2于B，C两点（点B在x轴上方）．