题目内容
已知抛物线C1:y2=4mx(m>0)的焦点为F2,其准线与x轴交于点F1,以F1,F2为焦点,离心率为| 1 | 2 |
(1)当m=1时,求椭圆的标准方程及其右准线的方程;
(2)用m表示P点的坐标;
(3)是否存在实数m,使得△PF1F2的边长是连续的自然数,若存在,求出这样的实数m;若不存在,请说明理由.
分析:(1)当m=1时,抛物线C1方程可知,所以,椭圆C2中c与a值可求,进而得出椭圆的标准方程及其右准线的方程.
(2)P点为抛物线与椭圆在第一象限的焦点,所以只要根据抛物线方程求出椭圆方程,再联立,即可得出P点坐标.
(3)先假设存在实数m,使得△PF1F2的边长是连续的自然数,由前一问可分别求出△PF1F2的三边长,让三边成公差为1得等差数列,求m的值,若能求出,则存在,若不能求出,则不存在.
(2)P点为抛物线与椭圆在第一象限的焦点,所以只要根据抛物线方程求出椭圆方程,再联立,即可得出P点坐标.
(3)先假设存在实数m,使得△PF1F2的边长是连续的自然数,由前一问可分别求出△PF1F2的三边长,让三边成公差为1得等差数列,求m的值,若能求出,则存在,若不能求出,则不存在.
解答:解(1)∵c1:y2=4mx的右焦点F2(m,0)∴椭圆的半焦距c=m,
又e=
,∴椭圆的长半轴的长a=2m,短半轴的长b=
m.
椭圆方程为
+
=1当m=1时,故椭圆方程为
+
=1,右准线方程为:x=4
(2)由
,解得:P(
m,
m)
(3)假设存在满足条件的实数m,由(Ⅱ)知P(
m,
m)
∴|PF2|=
m+m=
m,|PF1|=4m-|PF2|=
m,又|F1F2|=2m=
m.
即△PF1F2的边长分别是
m、
m、
m.
∵
-
=
-
=1∴m=3,
故存在实数m使△PF1F2的边长是连续的自然数.
又e=
| 1 |
| 2 |
| 3 |
椭圆方程为
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| x2 |
| 4 |
| y2 |
| 3 |
(2)由
|
| 2 |
| 3 |
2
| ||
| 3 |
(3)假设存在满足条件的实数m,由(Ⅱ)知P(
| 2 |
| 3 |
2
| ||
| 3 |
∴|PF2|=
| 2 |
| 3 |
| 5 |
| 3 |
| 7 |
| 3 |
| 6 |
| 3 |
即△PF1F2的边长分别是
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
∵
| 6m |
| 3 |
| 5m |
| 3 |
| 7m |
| 3 |
| 6m |
| 3 |
故存在实数m使△PF1F2的边长是连续的自然数.
点评:本题考查椭圆的几何性质,以及是否存在问题,做题时找准椭圆与抛物线的关系,认真解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•河北模拟)已知抛物线C1:y2=2px和圆
(2012•河北模拟)已知抛物线C1:y2=2px和圆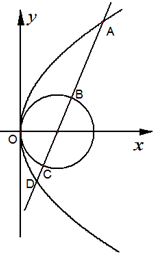 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).